Sluneční aktivita - Cykly

Hlavními cykly sluneční aktivity jsou Wolfův 11-ti letý a Haleův 22-ti letý cyklus.
Poslední maxima Wolfova cyklu byla v letech 1979, 1989 a 2000 (List_of_solar_cycles).

Viz také: Vliv planet na sluneční aktivitu.

Pozorování slunečních skvrn

Schwabe, Heinrich Samuel

Schwabe, Heinrich Samuel 1789-1875, amatérský astronom a botanik. Od r.1826 s věnoval (ve snaze najít intramerkuriální planetu Vulkán) detailnímu pozorování Slunce. Po letech pozorování si v r.1843 povšiml výrazné desetileté periody výskytu skvrn.

Schwabeova perioda

Perioda desetiletá

9.823563 let: S/3 (anomaliticky)
9.85 let: teplotní cyklus (New Haven)
9.885526 let: Ja/P (Fairbridge,1997), 9.9 let: cyklus v různých jevech
9.93-9.94 let: cyklus slunečních skvrn, délka slunečního cyklu (Charvátová)
10 let: Schwabeova aproximace Slunečního cyklu, atmosféra, rotace E (též variace pólu)
10.1466 let:9*1.1274 let, E-Měsíc
10.2 let: zimní teplotní cyklus (Hudson Valley)
10.2-11.0 let: geomagnetická aktivita, 10.2-11.2 let: skvrnová aktivita
10.0-10.3 let: jedna z period triády (Charvátová),
10.24 let = 4*2.56 let, bimodál sluneční cykly 10 a 12 let
10.4 let: silný roční teplotní cyklus (Hudson Valley), cyklus v letokruzích stromů (giant sequoia)
10.40 let: 52 let/5, 10.4163 let: B/41, 10.47 let: cyklus slunečních skvrn
10.54 let: ((J,S)/2,(U,N)), 10.566 let: ((J,S)/2,N)
10.8 let: vulkanická aktivita, 10.80774 let: 3/J-2/S=5.40387 let, 10.81254 let: Jakubowski
10.00 let: Wilson 1. mode (116-124 months)

>

Wolf, Rudolf

Wolf, Rudolf, 1816-1893, švýcarský astronom, organizátor prvního mezinárodního projektu sledování slunečních skvrn. Zrekonstruoval sluneční aktivitu zpětně až do r.1730 a upravil průměrnou periodu slunečních skvrn na cca 11 let.

Wolfova perioda

10.66 +- 0.02 let - dominantní periody slunečních skvrn z let 1700-2010 (J.E.Solheim)
10.7-11.5: změna výšky zóny skvrn (Gleissberg)
10.914 let: tritos = inex-saros (sluneční zatmění); 135 lunací (3987 dní)
10.97 let: 32.9 let/3, 11 let: inverze slunečního mg. pole, 10 oscillation years
11.01: 2*5.504 let (M-V interakce)
11.03-11.14 let (Schove 1955, za období cca 500 let)
11.0324 let: 31/2 tzolkin = 15.5*0.71177 let, 11.03295 let: (J,S) * 5/9; 11.03942 let: 9/J-25/S
11.04 let: Barnes,1980(±2.02 let)
11.05-11.09 – střední cyklus sluneční aktivity (Jakubowski), 11.0515 let: S*3/8; [18.62,27.19]
11.065 let: [J,5*32.9 let] = [J,164.5], 11.0657 let: [J,N] sidericky, maxima (Schove, přes 2000 let)
11.08 let: zrychlení a impulzy planet (R.Wolf), 11.0857 let: minima (Schove 1955, odvozeno from 1932-155.2*n)
11.095080 let: [3J,2S] = 9*1.2328 let =177.52/16, 11.09551 let: [J,(U,N)] anomalistic
11.1 let: obecně (Schwabe-Wolfova, Astronomie 1947), mezi maximy (Ellison 1958)
11.1188 let = 3/S-1/U = 1/(S,U)+2/S = 1/(S,U)+2/U, 1/11.1188-1/11.0657 -> H (2318 let)
11.121217 let: SSC, Sun-Spot-Cycle (Fairbridge,1997), 11.13: střední délka (Mirošničenko)
11.1426 let: (V/2, E'/3) = (0.61518/2, 0.94899/3)
11.1719 let: nodální cyklus měsíce Dione, 11.17 let: 178.73/16 = 279.3/25
11.19 let: minima sluneční aktivity, 11.20 let: Mirošničenko 1986; 7*(V,E)
11.2 let: sluneční aktivita (4.2 vzestup+7 sestup), <11.2 let: (A.Rima 1961)
11.214 let: 4096 dní =64*64 dní (čínský cyklus, viz 384 dní), 11.22788 let: 3/4*14.9705 let
11.233 let: ((J,S)/2, 170.8 let/2), 11.23845 let: (J,B/2) (anomaliticky)
11.261 let: ((J,S)/2,U), 11.274 let:10*1.1274 let, E-Měsíc, 11.30 let: Dvořák, 1989
11.34 let: (2071 dní) librace Galileových měsíců (Meeus)
11.3480 let: 16*Tzolkin = 8*1.4185 let, 11.3883 let: [J,24 J] = 16 tzolkin = 12*346.6314 d
11.4 let: cyklus slunečních skvrn (Winkless, Browning), sedimenty (R.J.Hugget), zákryty Měsíc-Saturn; [18.61 let,29.46 let]
11.42 let: (M/3,(Měsíc,E))= (87.969/3, 29.530588)= 4171.4 d
11.5 let: analýza dřeva ze Starého Řecka cca (-600,-400)
11.67 let: Wilson 2. mode (135-145 months)

Poloviční Wolfova perioda

Také uváděna jako 5-6 ti letá perioda Hellmannova.

5.125 let: teplotní cyklus (New Haven)
5.2 let: cykly v historii (N.S.Nesterov) (R.Tomes), 5.25 let: klimatický cyklus (de Boer, 1938)
5.504 let: 1/M-4/V+2/E+1/R (synchron. perioda h pro vnitřní planety)
5.5 let: atmosféra, rotace E (také variace pólů)
5.560608 let: JEV (Fairbridge,1997)
5.6 let: klimatický cyklus (Polli, 1950) , 5.6370 let:5*1.1274 let, E-Měsíc
5.7 let: cyklus in Cotton Acreage

Hale, George Ellery

Hale, George Ellery, 1868-1938, americký astronom, na základě pozorování magnetických polí na Slunci odvodil 22-letý cyklus.

Haleova perioda

22 let: sluneční skvrny, přepólování slunečního magnetismu, letokruhy
22.065 let: 31 tzolkin = 31*0.71177 let, 22.18 let: ((J,S),189.8 let) (tropicky)
22.40 let (67.2 let) 14 * (E,V) = Ts = 14*1.6 let,
22.422 let: Dicke,1979 (±0.036 let),
22.4558 let: 3/2*14.9705 let
22.462 let: ((U,N),(J,S)), osy [S,U][J,N] pravý angle (90˚) osy [J,S][U,N] angle 120˚.
22.5 let: cyklus povodňových hladin
22.56 let: N vztažený k (J,S)
22.58 let: ((J,S),N)
22.6002 let
22.75 let: sluneční cyklus (Winkless, Browning)
22.7766 let: 32 tzolkin = 32*0.71177 let
23.0 let: Haleův sluneční cyklus, cyklus v letokruzích stromů (Abbot)
23.2 let: seismičnost (+-6.4),
23.4 let: vulkanismus (+-6.0),
23.6 let: teploty

Abbotova perioda

44.45 let: [61.01,N]
44.77 let: V-E-J simulace, 4*11.19 let
45 let: zdvojený Haleův sluneční magnetický cyklus
45 let: sluneční cyklus (Precambrium)
45.2 let: cyklus úrovní povodní
45.5532 let: 64 tzolkin = 64*0.71177 let
46 let: klimatický cyklus, cyklus z letokruhů stromů (Abbot, 1937)
46 let: Merkurův transit přes Sluneční disk, 46=(6+7)+33=13+33 let
46 let: occultací of stars by the eclipsed Měsíc (65-19 let)

Gleissbergův cyklus

Cyklus sluneční aktivity, obvykle udáván jako 80-90-ti letý (70-100 letý) (Solar_variation),
objevený Wolfgangem Gleißbergem při výzkumu sluneční aktivity.
Gleissberg pozoroval 17 cyklů od roku 290 AD (s průměrným trváním c. 78 years) viz níže.
Délka cyklu není konstantní - významně se mění (přibližně 85 ± 15 let).

Chandlerova perioda

40.0 let: changes Chandler (S-Měsíc-E)
40 let: [60, 120]
40 let: intensita geomg. pole, archeomg. intenzita
40.50 let: rázy 779.94/365.256 = 15/7 (1.004);
40.66 let: konjunkce M-V-E vzory
40.67 let: 2*B/21 (anomaliticky)
40.7 let: spektrum sluneční aktivity (Vztahy S-Zeme III)
40.79 let: rázy 686.96/365.256 = 15/8 (1.003)
40.82 let: rázy ((M,V),(V,E)) (1:4)
40.84 let: rázy [E,V]/[E,M]=583.921/115.877=5.0391
40.85 let: beat(4/E-5/V+1/M) = 5*8.169 let
40.88 let: (E/8,R/15) tropicky
42.12 let: rázy from J/V = 19.282

Gleisbergova perioda

77 let: povodně na Nilu (Hameed, 1984)
78 let: isotopy kyslíku (Grónsko) (Dansgaard, 1973)
78.5 let: cyklus letokruhů stromů (a giant sequoia)
78.8 let: sluneční aktivita (Gleissberg)
79 let: sluneční cyklus (Precambrium)
80 let: letokruhy stromů v Californii (Maksimov, 1952)
80 let: úroveň Kaspického moře (Maksimov, 1952)
80 let: surovost zim (Evropa) (Maksimov, 1952)
80 let: Island - koncentrace ledu (Maksimov, 1952)
80 let: interdiurnální teplotní (Berkes, 1955)
80 let: cyklus v letokruzích stromů (14C)
80.427 let: (J/2,6.4 let)
83 let: sluneční aktivita (Wolf, 1853)
83 let: letokruhy stromů (sequoia growth per decade, Clough, 1933)
83 let: nízké hladiny Nilu (Clough, 1933)
83 let: surovost zim (Europe) (Clough, 1933)
83 let: E-J synodický násobek, 76*(E,J)
83.034 let: 7*J
83.4 let: Gleisberg cyklus (Fairbridge,1997)
84.0 let: sluneční aktivita (Maximov)
84 let: Beijing rainfall (Burroughs, 1992)
85.6 +-2.0 let: Dominantní periody ve spektru (J.E.Solheim, 2013)
85.7 let = (U,N)/2 = 171.4 let/2 konjunkce/opozice Uran-Neptun
86.124 let: 121 tzolkin = 121*0.71177 let
88 let: cyklus v letokruzích stromů (Japanese cedar tree)
88 let: polární záře, 89 let: klimatický cyklus
88 let: polární záře (north lights, polar flares)
89 let: Budapešť, Praha - klima (Thraen, 1949)
90 let: letokruhy stromů (Moseley, 1940; Lamb, 1972)
90 let: sucha (Moseley, 1944; Burroughs, 1992)
90.4 let: cyklus povodňových hladin
92 let: cyklus letokruhů stromů (Abbot)
95.8 let (191.6 let / 2) - dominantní cyklus ve slapovém spektru (E.Okal, Don L.Anderson, 1974).

Fáze

Poslední maxima Gleissbergova cyklu nastala přibližně v letech :
1710-1720, 1760-1770, 1840-1850 a 1950-1960.
Poslední minima Gleissbergova cyklu pak zapadají přibližně do let :
1740, 1810, 1900.

Tah Saturnu, Uranu a Neptunu

Konfigurace S-UN a SUN následují po sobě s periodou cca 18-21 let. Tedy interval dvou konfigurací SUN je 2x tak delší, tj. přibližně 40 let (např.1672-1630 nebo 1851-1810).
Uvažujme nyní konfigurace (ne nutně přesně zarovnané), při kterých planety S,U a N “táhnou proti” Jupiteru (jako tři muži s provazy) z protější strany Slunce.
Pokud povolíme širší úhly (max cca 60 dg od přesné opozice na obou stranách) rozšíří se seznam konfigurací J-SUN na (roky):
1630-1670-(1711), (1770)-1810-1850, 1950-1990-2030 .

Gleissbergovy extrémy

První 2 triády (1630-1711, 1770-1850) odpovídají Gleissbergovým extrémům:

1631 (1.10.1631)

1670 (1.4.1671)

1711 (1.6.1711)

1770 (1.1.1771)

1810 (1.11.1810)

1850 (1.8.1850)

Rok 1711

Rok 1711 zde označujeme (červeně) jako maximum, protože zakončuje Maunderovo minimum.
Ale někdy je považován spíše za minimum.
Tedy, pravděpodobně, jde o průchozí bod - viz graf z práce Prof.Silvie Duhau:

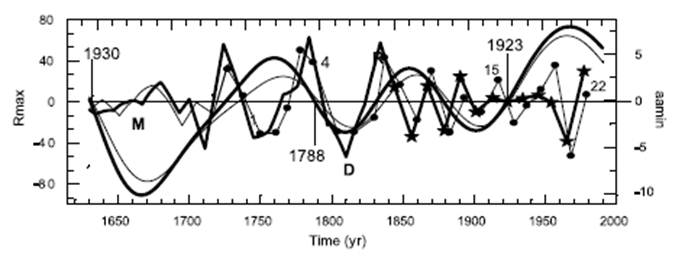
gleissberg01

Symetrické konfigurace

V některých případech jsou "provazy" planet Uran a Neptun téměř kolmé k "provazům" Jupitera a Saturnu. Například poblíž minima 1890-1910:

1890 (1.1.1890)

1910 (1.1.1910)

Zde jsou vypsány některé 100-leté intervaly, v nichž se neobjevuje žádná konfigurace J-SUN:
660-760, 840-940, 1020-1120, 1160-1270, 1350-1450, 1530-1630, 1670-1770, 1850-1950.

Obtížnost predikce

Zvláštní zarovnání v roce 1990 připomíná rok 1810, t.j.. Gleissbergovo minimum.
Ale byla aktivita v roce 1990 opravdu dlohodobým minimem? Máme očekávat maximum okolo roku 2030?

1950 (1.7.1950)

1990 (1.3.1990)

2030 (1.12.2029)

Historie

Tyto intervaly plynou z předcházejících schemat:
580-620-660, 760-800-840, 940-980-1020, 1120-1160, 1270-1310-1350, 1450-1490-1530,
(všimněme si Gleissbergových cyklů a některých 180-ti letých cyklů...)

Gleissbergovy extrémy

Gleissberg (1965)

Gleissberg	U#N	J - SUN
?	64	84
?	150	124
?	236	263
360	322	303
440	409	443
510	495	483
575	581	583
665	667	662
755	754	762
840	839	801
920	926	941
990	1011	980
1115	1098	1120
1185	1183	1174
1250	1270	1299
1305	1270	1299
1375	1355	1353
1455	1441	1453
1545	1527	1491
1605	1613	1632
1715	1698	1671
1765	1784	1771
1840	1869	1851
1955	1955	1950
?	2041	2029

Kondratievův cyklus

Přibližně 50-60-ti letý cyklus, obvykle citovaný jako 54-letý , viz Kondratieff cycles , Kondratiev wave .
Cyklus byl pozorován ruským ekonomem Kondratievem (Nikolai Kondratiev 1892-1938) a dále studován americkým ekonomem Deweyem (Edward R.Dewey, 1895-1978). Nabízí se souvislost s 55-letým cyklem sluneční aktivity.
Poslední extrémy Kondratievova cyklu byly přibližně v letech 1810,1865,1920,1975 (maxima), 1835,1890,1945,2000 (minima).
Cyklus 55-ti letý

Perioda byla pozorována v následujících jevech:

53.0 +- 0.6 let - dominantní periody slunečních skvrn z let 1700-2010 (J.-E.Solheim)
53.2 let: cyklus v letokruzích stromů (obří sekvoje)
53.3 let: 5*10.66 let (J.-E.Solheim)
53.38 let: 9*J/2; B/8; 75 tzolkin
53.5558 let: 8/S-3/J, rázy (J/3,S/8) - zhruba 268 let/5 = 53.6 let
53.9 let: ze spektra sluneční aktivity (sborník Vztahy S-Zeme III)
54 let: Kontradiev - ekonomický cyklus (54 let=270 let/ 5)
54.093 let: Exeligmos=3*Saros, cyklus sluneční zatmění =669 lunací =19756 dní
54.91 let: ze spektra sluneční aktivity
55 let: cyklus v letokruzích stromů (Japonský cedr)
55.24 let: konjunkce Jupiter-Uran, 4*(J,U)
55.33 let: M-V 224.701/87.969 = 2.5543 23/9 rázy
55.408 let: [U,N] (tropické periody), 55.6449 let: [U,N] (siderické periody)
56.1 let: cyklus slunečních skvrn
56.64 let: 1/J-3/S+3/U-3/N

Martin Roy o sluneční aktivitě

Opozice Jupiter-Uran

Průměrná perioda 4 konjunkcí J-U je 4*(J,U)=4*13.81=55.24 let:

Minima

29.4.1893 27.7.1948 31.10.2003

Maxima

16.12.1920 14.3.1976 12.6.2031

(http://dollarcollapse.com/wp-content/uploads/2010/05/Kondratieff.jpg)

110-letá perioda a její násobky

Cyklus 110.5 let

Perioda 10 W ~ 110.3-110.6-letá se objevuje v opakování opozic VEJ proti U (např. okolo 1727.87, 1838.17 nebo 2058.7).
Dělitelem periody 110.5 let je - kromě periody (J,U) - také perioda cca 10.05 let synodických (V,R),(R,S) a (V,S) (ve vztahu ke slunečnímu maximu r.1727.1). 110.31: V-E-J simulace 2*44.77+20.77 let, 10 * 11.031 let110.500 let: 8*(J,U) = 8*13.8125 (317.77/3 = 105.923 let)111.050 let: Měsíční slapový cyklus (Wood) 112 let: 4*28 let, "kalendáře povětrnosti", "stoletý kalendář" Woodova rezonance

Rok	∆L_JU	L_W[˚]
643.85	3	9
753.59	-4	10
863.92	-1	9
974.97	-5	-7
1085.42	-9	2
1195.35	-9	-2
1306.56	0	-8
1416.79	-5	-9
1527.02	4	-9
1637.71	-5	-9

Nechť L_w = 3*L_V-5*L_E+2*L_J [˚]. Perioda Woodovy rezonance činí 11.06753. Tedy s periodou 8*(J,U) ~110.5 let se vrací hodnota L_w k ~0˚:

(V/3,-E/5,J/2) = 22.135 let = 110.68 let/5

Rezonance E-R

Rok	∆L_JU	L_ER[˚]
1278.11	-4	-2
1389.38	-1	-10
1499.69	-5	-8

(E,R/2) = (1.00000,1.88085/2) = 15.781 let = 110.47 let/7

Synchronizace J-U a R-S?

Synodická perioda (R,S) = 2.009131627 zapadá (55 násobkem) do 110.5- ti leté periody. 16.12.1920
Opozice R-S se kryjí s opozicemi J-U v letech:

594.9, 705.47, 815.99, 926.48, 1036.96, 1147.48, 1257.98, 1368.46, 1478.97, 1589.47, 1699.95, 1810.46, 1920.96, 2031.45, 2141.95. Některá z dat (např. 1699.95, 1810.46, 1920.96) ukazují k obdobím lokálně nižší Sluneční aktivity. Poslední známý pokles Sluneční aktivity je z počátku 20-tého století.

Konjunkce J-X

Periodu 110.5 let pokrývá přibližně 9 konjunkcí J-X (viz Planeta X)

9 * (J,X) = 9*12.2368 let = 110.13 let

Např. 1686,12 ( 12,27) 1698,38 ( 12,27) 1710,65 ( 12,24)

1722,89 ( 12,27) 1735,15 ( 12,24) 1747,39 ( 12,24)

1759,63 ( 12,21) 1771,84 ( 12,21) 1784,05 ( 12,21)

1796,26

31.1.1686 13.6.1796

Cyklus 190 let

190.0 +- 9 let - dominantní cyklus ve spektru délek slunečních cyklů (J.-E.Solheim, 2013).

Cyklus 208 let

Tzv. cyklus "de Vries" (McCracken, 2013)

Cyklus 221 let

Timo Niroma: „200-210 a 1000-1050 let se zdají být největší známé oscilační periody Sluneční intenzity. Také se zdají ovlivňovat teploty na Zemi. V průběhu posledních 400 let se zdá být velká podobnost mezi Wolfovými čísly vzdálenými 221 let (horní limit 200-letého cyklu?).“

220 let ve spektru sluneční aktivity (Vztahy S-Zeme III).
220.55 let: 9*(U,N)/7 (anomaliticky)
222.019 let: Woodův měsíční slapový cyklus (Fairbridge,1997)
222.6 let: ((J,S/2),U) = (60.85,83.75) (anomaliticky)

Výrazná deštivá období

Zdeněk Vašků publikoval (r.1997) podrobnou analýzu deštivých období posledního tisíciletí. Poukázal na existenci čtyř výrazných období (tzv. “malých pluviálů“ I.-IV.) a předpověděl existenci dalšího období na roky 1995-2035), viz Naše malé pluviály. Periody dobře zapadají do cyklu 221 let:

Viz také: Obálkové funkce.

Deštivá období

Opozice J-U Deštivá období
---------------------------------------------

898.86 898 Nov 5 ?

1119.83 1119 Oct 23 1078-1118

1340.85 1340 Oct 27 1310-1350

1561.84 1561 Oct 22 1560-1600

1782.83 1782 Oct 27 1763-1804

2003.84 2003 Oct 31 1995-2035

2224.83 2224 Oct 26 ?

23.10.1119 27.10.1340 22.10.1561

27.10.1782 31.10.2003 26.10.2224

Cyklus 331.5 let = 2*165.75 let

Neptunova oběžná perioda odpovídá přibližně12-ti periodám (J,U) a 13 periodám (J,N) : 164.77 let: N165.25 let: (W,J) = (11.06753, 11.861983) , viz Woodova rezonance 165.5 let ± 0.5 let: odchylka těžišť soustavy Slunce-JSUN a soustavy Slunce-JS165.75 let: 12 * (J,U) = 12*13.812; 166.17 let: 13 * (J,N) = 13*12.782332.27 let: Rázy 4/(J,S) – 9/(S,U) = 4/J – 13/S + 9/U = 1/332.27 let334 let: klimatický cyklus (Auric, 1936)

Cyklus 442 let

Blízká přiblížení Země a Marsu nastávají přibližně v intervalech 47 let, 79 let, 205 let (=2*79+47), 284 let (=3*79+47) apod.
V řadě 1119,1198,1403,1482,1561,1640,1845,1924,2003 se roky 1119, 1561, 2003 (v odstupu 442 let) kryjí s opozicemi J-U.
V těchto letech prochází Saturn přísluním, perioda 15*S =15*29.4572 let =441.86 let.

Cyklus 554 let

Cyklus sluneční aktivity (intenzivní maxima) pozorovaný J.Schovem.

Cyklus 884 let

Perioda 884.1 let je násobkem periody 5*S, 884.1=6*147.35 let, 30*S=30*29.457=883.715 let, 64*(J,U) = 64*13.812 = 883.965 let, 139* I = 139*6.3611 let = 884.193 let. Poměr S/J odpovídá poměrně přesně 149/60, tedy 30*S = 44.5 (J,S) = 74.5 J = 884.1 let.
Opozice V-ER a zároveň opozice J-U nastávají přibližně 17.7.235, 31.7.1119, 31.7.2003, 16.9.2887,…
Perioda 884.1 let je pozorována v současných opozicích (V -ER) a (J-U). Saturn poblíž perihelu. Perioda 884.1 let odpovídá také 49 periodám Saros (18.03 let).

23.10.1119 22.10.2887
syst11190813

Cyklus 1216 years

Podle analýz v projektu (Charvátová,Střeštík) je významnou klimatickou periodou 1214 let. Povšimněme si, že 1215.5 let = 11 * 110.5 let. Přesné konjunce V-E-R nenastupují vždy po cca 300 letech, perioda se mění v rozpětí cca 298.9-318.2 let (298.9 let ~ 47*6.4-1.88 let, 318.2 let ~ 50*6.4-1.88 let). Např. E-V-R najdeme v jedné přímce v letech 1044.05,1343.00,1661.19,1960.13,2259.09; rozdíl 2259.09-1044.05=1215.04 let.

Cyklus 1768 years

Podle 1767.4 let: 2*883.7 let=3*589.1 let = 17* 103.96 let = 89 * 19.859 let. (Jestliže v konjunkcích V-E-R vypadne každých cca 300 let jedna perioda Marsu, je to jako jedna Wolfova perioda v průběhu 1768 let…)

Stadiální cykly

V souvislosti s cykly ledových dob (stadiálními cykly) bývá zmiňována trojice period 550 let–1100 let–1650 let.

Odraz násobků cca 280-ti leté periody v klimatických oscilacích (Stacey, Karlstrom,..):

Cyklus 280-ti letý

278.0304 let: 14SJ/EV (Fairbridge,1997) 280 let: biologický cyklus (letokruhy stromů) 280.054 let: 2*140.027 let 283.0 let: změny ledovců (glacier-iceberg) 284.7075: Mayský cyklus, zlomek Babylonského cyklu, 24*J= 2*B/3 = 400 tzolkin (151 R) 285.0 let: (32.87, S) 286.1 let: E-R cyklus, 7* 40.876 let 286.96 let: 8*(S,N) = 8*35.87 let 290 let: sluneční cyklus (stará čínská pozorování) Pětilístkový pohyb Slunce?

Siderické periody vnějších planet splňují rovnici (viz Stabilní rezonance ):

3/J-8/S-2/U+7/N = 0

Ke vztahu 8/S-3/J=5/G existuje analogický 7/N-2/U=5/G a oba se skládají do rovnice (8/S-3/J) - (7/N-2/U) = 0, která platí, alespoň co se průměrných period týče, velmi přesně.

Odtud vychází G=267.67-267.78.

Co když pohyb Slunce-J-S není trojlístkový, ale pětilístkový (vzhledem k pomyslné periodě G, ať už je tvořena čímkoliv…) s rezonancí S:J nikoliv 5:2, ale 8:3 ?

Vzhledem k periodě G=270-285 let tvoří synodické periody (S,G):(J,G) poměr 8:3;

(J,G)=12.4 let (viz P.Kalenda,J.Málek:teorie slun.dynama)(S,G)=33.0 let (3 Wolfovy cykly).

Indicie pro pětilístkový pohyb

když se cca r.2003.7 (18.8.2003-31.8.2003) zarovnaly planety do přímky podle minimální interakce, byl odstup Jupitera od Saturna cca 54˚, tj. (360˚+180˚) /10.Landscheidtova pětidílnostpozorování cca 270-ti leté periody v slapové teorii (viz P.Kalenda,J.Málek:teorie slun.dynama)pozorování posuvů 180-ti letých cyklů se synchronizací po cca 2*270-ti letech (P.Kalenda)

Stacey‘s cycle

536.2 let: 3*178.73 let
536.2 let: vzájemný pohyb J-S-Hidalgo, 7* 76.6 = 7*(J, Hidalgo) = 20*26.81 = 20*(S, Hidalgo),
537.0 let: rázy 3/J-2/V+3/E
540-580 let: Pearsonův-Staceyův cyklus
550.0 let: Feirbridgeův cyklus 550,1100,1650 (3600) let
556 let: Staceyův - Zero-check cyklus/3, (539.8-556.0, mean 548 let)
556 let: násobek konjunkcí J-S (28*19.86=3*185.3)
556.027 let: postup měsíčního perigea (Fairbridge, Sanders)
556.0609 let: SQ-1 (Fairbridge,1997)
558 let: měsíční slapový cyklus (Wood)
560 let: S-U perturbace (Schlyter)
566.58 let: (S,U/3) (anomalisticky)
567 let: Pearsonův geologický cyklus
570 let: teplotní cyklus, geologický cyklus (pískovcové útvary)

Karlstromův stadiální cyklus

1112 let: Staceyův cyklus, (anomalisticky)
1118.23 let: Jakubowski - model sluneční aktivity
1133.0 let: Karlstromův stadiální cyklus

Petterson‘s tidal cycle

1665.7 let: 9/25 *4627 let = 9* 185.08 let
1668.1825 let: SQ-3 (Fairbridge,1997)
1668 let Staceyův Zero-check cyklus 3*556 let, Země-Měsíc, 84*(J,S)
1700.0 let: geofyzikální cyklus změny ledovců
1700 let: pohyb ledovců (Pleistocene)
1703.5 let: nerovnosti (544.79,800.94) (tropické periody)
1708 let: 5125 let/4 (cyklus odvozený z Mayského), 4*B = 144*J=1708.245 let
1708 let: velké erupce sopek (-3341 Avelino,-1633 Thera,+75 Vesuv,+1783 Laki)

Karlstromův velký cyklus

3336.365 let: SQ-6 (Fairbridge,1997)
3400.0 let: Karlstromův cyklus ledových dob