Rezonance

Úvod

Lineární rezonance

Soustava period T_i rezonuje, jestliže existují taková celá čísla a(i), že platí:

|∑a_i/T_i| < α

kde i=1..n, α je nějaké malé číslo. Hodnota 1/α je perioda: T = (T₁/a₁,T₂/a₂,T₃/a₃,...) = 1/(a₁/T₁+a₂/T₂+a₃/T₃...) = 1/α

Např. pro periody J=11.862 a S=29.457 let při a1=2, a2=-5 dostaneme: α = 2/J -5/S = 0.001133, tj. T =1/α = (J/2,S/5) = 883 let.

Řád rezonance

Řádem lineární rezonance se obvykle rozumí číslo:

k= ∑|ai|

Tedy např. poměr 2:1 je řádu 3, 3:2 řádu 5 a 4:3 řádu 7. Tato definice řádu rezonance je jednoduchá, slouží spíše jen pro orientaci.

K posouzení kvality resonance nestačí (viz porovnání s hudbou – kvalita hudebních intervalů apod.)

Rezonance a hudební teorie

Zatímco hudba postrádá gravitační zákon (vazba citlivých tónů je ale obdobou gravitační vazby …), předchází výzkum hudebních jednoduchých poměrů (konsonantních intervalů a soustav ladění,…) astronomii o kus cesty. V hudebních rezonancích mají zvláštní význam násobky čísla 2 (oktávová identita). Vylaďováním učitých poměrů se jiné rozlaďují (ladění je vždy určitý kompromis). Hudba je střídáním stabilních (rezonančních) a nestabilních (dočasných, chaotických) útvarů. Hudební systémy (např. 12-ti tónový) jsou postaveny tak, aby stabilní útvary mohly vznikat.

Typy rezonancí podle period

Nechť P je označení planety nebo planetky a M měsíce; P, M jsou orbitální periody, Pr, Mr rotační periody.

Podle kombinace P,Pr,M a Mr rozlišíme 10 typů rezonancí.

Nelineární rezonance

Nelineární rezonance závisí nejen na periodách, ale také na amplitudách dílčích pohybů.

Rezonance oběžných dob

Rezonance oběžných dob

Nejjednodušším případem rezonance je celočíselný poměr dvou oběžných period:

P/Q = n

Triviálním případem rezonance tohoto typu je rezonance 1:1, např.:

• vázaná rotace měsíců planet (náš Měsíc, galileovské měsíce Jupitera, ...)
• pohyb těles v Lagrangeových bodech (Jupiter-Trojané, Dione-Helene, ..)

Existenci jednoduchých poměrů ve Sluneční soustavě analyzoval A.M.Molčanov (r.1968) použitím statistické analýzy. S.F.Dermott (r.1969) se pokusil vyjádřil poměry oběžných period celými čísly. Podle Molčanova se libovolný nelineárně kmitající systém se dostane do synchronizovaného režimu pohybů (v důsledku evoluce) i při působení velmi slabých vazeb.

Rezonance s oběžnou periodou

V některých případech je pohyb jednoho tělesa tak výrazný, že zcela ovládá pohyb jiného tělesa Například Jupiter ovlivňuje pohyb tisíců planetek a komet.

Nechť P,Q jsou siderické periody dvou těles. Rozlišujeme 2 případy:

(Q,P) = r∙P

A/

Odtud P/Q = (r+1)/r. Např. pro P=J a Q=A, kde J je perioda Jupitera a A perioda asteroidu, viz dále v kapitole Působení Jupitera.

Pro celočíselné r neexistují stabilní kruhové dráhy (H.Scholl). Eliptické dráhy mohou být stabilní i nestabilní (J.D.Hadjidemetriou).

(Q,P) = P/r

B/

Odtud P/Q = r+1.

Stáčení rezonanční přímky

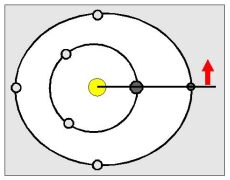
Celočíselné poměry se v poměru period (těles Sluneční soustavy) zpravidla nerealizují přesně, cykly jsou obvykle modulovány jinými cykly. Tento složitější případ bývá zahrnován pod pojmem sekulární rezonance.

V případě pohybu 2 oběžnic okolo centra bývají rozlišovány dva typy rezonancí:

Má-li jedno z těles výraznější excentricitu, nastává tzv.rezonance excentricity (např. v párech Enceladus-Dione, Titan-Hyperion, asteroid Hilda-Jupiter)

má-li výraznější sklon objevuje se tzv.rezonance sklonu (např. Mimas-Tethys).

Oba typy (včetně jejich možné kombinace) se zdají být jen různým projevem téhož principu: konjunkce těles nastávají vždy poblíž bodu, kdy jsou příslušné oběžné dráhy nejvzdálenější.

Laplaceova rezonance

V případě 3 oběžnic je nejvýraznějším projevem tzv. Laplaceova rezonance (Io-Europa-Ganymed, Miranda-Ariel-Umbriel). V tomto případě nedochází nikdy ke konjunkci všech tří těles zároveň. (Obdobnou souvztažností se zdá být vázána i rotace Venuše k oběžným dobám Venuše a Země.)

Laplaceova rezonance

Nechť P,Q,R jsou siderické periody tří těles a p,q,r celá čísla.

Tzv. synchronizační (Laplaceova) resonance je určena vztahem:

I= (Q/q,P/p) = R/r

Rezonance narušuje pravidelný pohyb měsíců. Silné ovlivňování měsíců působí obtíže ve výpočtech (Wargentin, Lagrange,Laplace, Souillart).

Zvláštní případ: r=1, p=q-1. Tj. 1/R-q/Q+(q-1)/P = 0 a odtud (R,Q/(q-1)) = (Q,P/(q-1)) a (Q,P) = q∙(R,P) kde q>1.

1/I-3/E+2/G=0

Perioda nerovnosti I dvou těles je celočíselným dělitelem orbitální periody třetího tělesa.

Tělesa se vyhýbají vzájemně, např:

(Zvláštní případ - jedna perioda je rotační.)

Jiné rezonance

Rezonance Uranových měsíců

V soustavě měsíců Uranu (Miranda - Ariel -Umbriel - Titania) se objevuje dvakrát obdobný vztah (nestabilní rezonance):

4/P-8/Q+3/R=0

1/ pro Mirandu,Ariel a Titanii (M/4,-A/8,T/3) 2/ pro Ariel, Umbriel a Titanii (A/4,-U/8,T/3).

Obdobný vztah platí také pro Zemi, Mars a Jupiter (E/4,-R/8,J/3) ≈ 1782 let.

Mocninná rezonance

Resonanční podmínka v magnetické smyčce: ω = sqrt (ω_a² + ω_b²)
Tedy, nechť 1/f(A,B) = 1/f(A) - 1/f(B), kde P' = f(P) = sqrt(p)

   (V,E) = 13.227 let 
   (E,R) = 13.633 let 
   (V',-E'/2,R') = 0

   (R,S) = 3.3678 let 
   (V,R) = 3.357 let

   (J,S) = 88.830 let (J,U) = 30.438 let 
   (J,N) = 22.157 let (S,U) =177.050 let 
   (S,N) = 88.420 let 
   (J',-S',N') = 0

Stabilní rezonance

Lineární rezonance je považována za stabilní, když

∑a_i = 0

(ve smyslu předchozího označení). Mějme n-period P_i: {P0, P1,..., Pn} v soustavě P. Pro pozorovatele ze soustavy Q, jejíž perioda pohybu vzhledem k soustavě P je M, se tyto periody jeví jako (P_i,M), tj. {(P0,M), (P1,M)..., (Pn,M)}.

Synodické periody pozorované ze soustavy Q jsou stejné jako synodické periody pozorované uvnitř P:

((P_i,M),(P_j,M)) = (P_i, P_j)

(Totéž neplatí pro periody osové).

Pro libovolné konstanty a(i) je

∑a_i/(P_i,M) = ∑a_i/P_i – (∑a_i)/M.

V případě stabilní rezonance ∑a_i/M= 0 dostaneme:

∑a_i/(P_i,M) = ∑a_i/P_i

tedy stabilní rezonance je nezávislá na volbě vztažné soustavy.

Například periodu H rezonance 1/J-3/S+1/U+1/N = 1/H naměří také pozorovatel pohybující se s libovolnou periodou M (vzhledem k hvězdám): 1/(J,M)-3/(S,M)+1/(U,M)+1/(N,M) = 1/H, protože 1/J-3/S+1/U+1/N je stabilní (1-3+1+1=0).

Triviálním případem stabilní rezonance je synodická "rezonance" 1/P-1/Q=0, 1-1=0 (pro P=Q).