Za příčinou sluneční aktivity
Úvod
Cílem následujícího pojednání je ukázat některé možné souvztažnosti mezi pohybem planet a pozorovanou sluneční aktivitou. Předpokládáme, tak jako již na samém začátku systematického pozorování v 18.století Rudolf Wolf, že hlavním motorem působení je planeta Jupiter, a že vliv této planety se dále kombinuje s působením dalších planet, přičemž o delších cyklech rozhodují především vnější planety. Mezi těmito má potenciálně největší vliv Saturn, což naznačil již anglický matematik a astronom E.W.Brown v r.1900 a později (v r.1930) se snažil dokázat americký matematik (irského původu) W.A.Luby.
Na skutečném průběhu cyklu se podílejí pak i další planety a tělesa, přičemž pohyb těch vzdálenějších se promítá do vedlejších (sekulárních) cyklů aktivity, zatímco menší a ke Slunci bližší planety modifikují průběh cyklu jen v krátkých časových intervalech a mohou se podílet nanejvýše na některých lokálních extrémech aktivity. Pokud se pozoruje soulad pohybu Slunci blízkých planet s primárním Wolfovým cyklem aktivity, považujeme to spíše za výsledek synchronizace všech těles soustavy - která nastává nutně proto, že se Slunce snaží minimalizovat svůj pohyb okolo těžiště (barycentra) všech těles, které okolo něj obíhají, a také v důsledku "odpuzování" těles na blízkých drahách, který dává vznik rezonancím.
Některé výchozí úvahy přebíráme od českých teoretiků - I.Charvátové (uspořádaná a chaotická období aktivity) a P.Kalendy (působení těles na eliptických drahách). Ve správnosti předkládaných vztahů se dále utvrzujeme tím, že pokrývají myšlenky dalších badatelů - např.finského klimatologa Tima Niromy (působení Jupitera v perihelu) a australského klimatologa Iana Wilsona (působení planet v kvadraturách). Na potenciální souvislosti s pracemi dalších vědců upozorníme až dále v textu.
V textu se také pokusíme vyrovnat s námitkami proti planetární teorii sluneční aktivity. Některým námitkám je oponovat těžké, ale například kritiku G.F.Kronenbergera z r.1913 je možné na základě předkládaných vztahů vyvrátit poměrně snadno. Zároveň ale ukážeme i situace resp. období, která předloženými vztahy vysvětlit nedokážeme.
Základní myšlenkou je v našem pojednání představa, že Sluneční aktivita je produktem více dějů, které se ne vždy dokonale skládají, ale - z dosud ne zcela známých příčin - střídavě vystupují do popředí nebo ustupují. Ukážeme dvě funkce s blízkými periodami, které jsou odvozené přímo z pohybu těles Jupiter a Saturn a odpovídají vztahům navrženým E.W.Brownem v r.1900 a které nedávno znovu oživil americký vědec (srbského původu) M.A.Vukčevič.
Při porovnávání navržených funkcí s jevy pozorovanými na Zemi se ukázala pozoruhodná shoda mezi minimy funkcí a většími geologickými událostmi na Zemi. Tuto závislost bude nutné statisticky doložit, což není předmětem naší práce, ale v některých případech se zdá naprosto zjevná. Velké geologické události (erupce sopek, zemětřesení) se často objevují v krátkém časovém intervalu po konjunkci nebo opozici Jupitera se Saturnem v blízkosti perihelu Jupitera. Takové uspořádání nastává cca s periodou 60-61 let, v důsledku blízkosti period obou funkcí se ale může objevit velmi přibližně i o cca deset let dříve nebo později (od přesného zarovnání). Tuto závislost sledují obdobně nejen geologické ale i klimatické a potenciálně geomagnetické jevy - např.bouře na moři pozorované v letech 1099, 1526 a 1953, jak bude ukázáno v odstavcích o Babylónské periodě (427 let = 7 * 61 let).
Vliv planet na Slunce
Faktory působení
Negativní faktory
Mezi jevy, které sluneční aktivitu snižují se obvykle počítají konjunkce (někdy i opozice) vzdálených velkých planet. Protože konjunkce nejen navyšují sílu směrem ke Slunci, ale i vychylují polohu Slunce vzhledem k barycentru, považuje se někdy za příčinu poklesu aktivity toto vychýlení a tím neuspořádanost pohybu ve sluneční soustavě (I.Charvátová).
Rozšíříme-li jev konjunkce na více těles, mluvíme o směrovém "zahuštění". Působení více těles v jednom určité sektoru může mít větší efekt než prostá konjunkce. Takové zahuštění může v určitých obdobích narůstat souběžně s tím, jak se tělesa postupně (od vzdálených směrem k Slunci bližším) dostávají do vzájemných konjuncí.
V blízkém okolí roku 1306 kdy se setkávají vnější planety (J-S-U-N) v poměrně úzkém sektoru byla (např. podle Schove) nižší sluneční aktivita a celé širší okolí bývá nazýváno Wolfovo minimum (na obrázku poloha planet 15.8.1306).

A obdobně - rok 1810 bývá považován za rok bez aktivity. V tomto roce nebyla pozorována prakticky žádná sluneční skvrna. Jeho širší okolí bývá nazýváno Daltonovo minimum. Následuje cca 504 let po roce 1306, což je mimo jiné doba, se kterou planety Saturn, Uran a Neptun - spolu i s Plutem - přibližně opakují polohy.
K uvedeným faktorů přistupuje ještě jedna věc, která má pro naše další úvahy zásadní význam: Efekt podobný konjunkci planet může vyvolat i jediné těleso na eliptické dráze, přibližování tělesa k perihelu je analogické konjunkci s jiným tělesem (P.Kalenda).
Pozitivní faktory
Pozitivní faktory jsou inverze faktorů negativních. Jako nejvýraznější z nich vystupují tzv.kvadratury planet, to je okamžiky, kdy úhel P-o-Q (kde P,Q jsou planety a "o" představuje Slunce) je pravý.
Kvadratury planet do výpočtů extrémů aktivity započítal již v 60-tých letech 20-tého století P.R.Romančuk (Univerzita Kiev), v dalším desetiletí pak ve společné práci i H.T.Mörth (Anglie) a L.Schlamminger (Německo). Později na význam kvadratur upozornil také Ian R.G. Wilson.
V Mörth-Schlammingerově teorii se uvažuje především o kvadraturách párů Jupiter-Saturn a Uran-Neptun. Odstupy prvních z nich činí v průměru 19.86/2 = 9.93 let, odstupy druhých v průměru 171.4/2 = 85.7 let. Skutečné odstupy kvadratur se od průměrných odstupů pravidelně odchylují, u kvadratur Jupiter-Saturn v cyklech s přibližně 60-ti letou periodou.
Jakkoliv se zdá být jev kvadratur důležitý, není možné jím vysvětlit celá souvislá období. Vysvětlení, že je jev kvadratur komplexnější a je například složitější závislostí goniometrických funkcí pohybu planet, nebo že je ovlivněn modulací apod. se nepodařilo nijak potvrdit.
Podle umístění těles můžeme rozlišit dva typy kvadratur:
-
1. Před konjunkcí těles (rychlejší těleso vzadu),
pro J-S např. 1778, 1837, 1958, pro U-N, 1778, 1947, 1958. -
2. Po konjunkci těles (rychlejší těleso vpředu),
pro J-S např. 1727, 1947, pro U-N 1870.
Potenciálně výrazným jevem se zdá být i zmíněné působení eliptických drah. V některých obdobích koreluje vyšší sluneční aktivita s pohybem planet poblíž afelů. Jako zde v období cca 1940-1985 extrémy (1947.5, 1957.9, 1968.9, 1979.0) u afelů Jupitera (1945.93, 1957.81, 1969.67, 1981.58):

Kvadratury se po roce r.1750 resp. r.1940 vytrácejí (stávají se nepřesnými). Zároveň však začíná období zvýšeného vlivu eliptické dráhy Jupitera!?
Pro období 1700-1980 platí zhruba pravidlo, že v okolí opozic Uran-Neptun (1710-1750, 1890-1940) se sluneční aktivita řídí kvadraturami Jupiter-Saturn, v okolí konjunkcí (1770-1830,1950-1980) pak afelem Jupitera. Pro jiná období však stejné pravidlo, zdá se, neplatí.
Gnevyševova mezera
Gnevyšev ukázal, že maxima (v zelené čáře 5303 Å) okolo roku 1958 byla dvě - první v roce 1957, druhé o 2-3 roky později. Časový interval mezi těmito dvěma daty se nazývá Gnevyševova mezera. Podle výše zavedených funkcí dostáváme v tomto cyklu také dvě maxima - ale poněkud dříve: maximum od kvadratury Jupiter-Saturn v r.1955.98 a maximum od afelu Jupitera r.1957.81. Toto naposledy jmenované odpovídá prvnímu Gnevyševovu maximu. Druhé Gnevyševovo maximum připadá spíše až na okamžik konjunkce Jupiter-Saturn. Do celého intervalu se promítá také kvadratura Uran-Neptun (cca 1955.3) .
Působení kvadratur Jupiter-Saturn
Vysoké extrémy sluneční aktivity v letech 1727 a 1837 jsou těsně předcházeny kvadraturami Jupiter-Saturn (1727.50-1727.39=0.11 let, 1837.20-1836.99=0.21 let).
29.6.1727
 11.03.1837
11.03.1837

V období 1900-1940 nastávají extrémy (1907.0, 1917.6, 1928.4, 1937.4), přibližně v kvadraturách (1905.82, 1916.36, 1926.65, 1936.07):

Totéž nastává i v období 1710-1750. Cykly sluneční aktivity zde postupují téměř synchronně s cykly Jupiter-Saturn s extrémy (1718.2, 1727.5, 1738.7, 1750.3) v kvadraturách (1717.70, 1727.25, 1737.57, 1748.06):

V datech extrémů sluneční aktivity podle Schove postupují sluneční cykly synchronně s kvadraturami v obdobích: 10-40, 120-150, 195-240, 385-430, 555-605, 655-675, 715-765, 960-1005, 1150-1200, 1360-1400, 1430-1460, 1515-1560, 1715-1750, 1885-1950.
Působení Jupitera v afelu
S rokem afelu Jupitera se shodují i některé starší (historické) záznamy o pozorovaných slunečních skvrnách - např. z r.807 (afel 807,1), 829 (830,83) ,1198 (1198,64).
V datech extrémů sluneční aktivity podle Schove postupují sluneční cykly synchronně s afelem Jupitera v obdobích: 95-155, 330-360, 440-465, 500-570, 710-750, 805-830, 925-1000, 1130-1190, 1350-1360, 1400-1415, 1515-1530, 1610-1625, 1775-1830, 1955-1980.
Kombinace vlivů
V období 1750-1820 se působení eliptických drah nezdá působit samostatně. Skládá se s efektem kvadratur Jupiter-Saturn!?:

Chybějící maximum!?
Na předchozím obrázku se ukazuje jedna pozoruhodná věc. Spojením obou pozorovaných vlivů do extrémů okolo r.1787 (max 1788.1) a r.1807 (max 1805.2) zůstal jeden cyklus kvadratur - s extrémem poblíž r.1797 volný -jakoby nepokrytý sluneční aktivitou. To je zřejmé i z následující tabulky:
Jupiter v afelu Extrém aktivity Kvadratura J-S
----------------------------------------------------
1791,73 1788.1 1786,20,
- - 1797.18
1803.61 1805.5 1807.58
|
Poloha planet na začátku roku 1797 
|
A je to právě rok 1797 (popř. roky 1796-1797), o jehož správné zařazení se vedou mezi vědci polemiky. Je v něm (původně opominuté) maximum křivky aktivity nebo není? Chování pozorovaného 22-letého Haleova cyklu zde totiž vykazuje (ve srovnání s jinými obdobími) odchylky a dochází k porušení pravidla Gnevyšev-Ohl.
Z uvedeného grafu vidíme, že v r.1797 je maximum kvadratur, ale je oslabené - není jako v období před ním a po něm posílené afelem Jupitera. V okolí roku 1797 není navíc poblíž perihelu jen Jupiter, ale i Saturn s Uranem.
Podobný typ extrémů jako v letech 1788 a 1805 najdeme například r. 1718, 1848, 1907 a podobný typ extrému jako r.1797 vychází na roky 1857, 1916 (nastal 1917.6) a 1975.
Nárůst aktivity v období 1760-1780 resp. 1940-1960 je potenciálně posílen kvadraturami Uran-Neptun. Přitom body zlomu v okolí r.1762 resp. r.1941 odpovídají konjunkcím Jupiter-Saturn-Uran.
Sluneční aktivita tedy nemusí být výsledkem jednoho typu působení, ale možná střídáním několika takových, podle toho, jak se polohy planet v čase proměňují. V různých obdobích získávají různé projevy více nebo méně na síle, ukazují svůj vliv a pak se zase vytrácí.
Na projevy této společné podstaty se dále podíváme o něco detailněji.
Vlastní funkce
Všechny výše uvedené faktory působení vycházejí ze stejného základu: zvýšení gravitačního vlivu na Slunce (po určitou dobu) vede obecně ke snížení aktivity, uvolnění tohoto vlivu aktivitu zvyšuje.
Jak odvodíme funkce, které se ukazují v grafech? Černá křivka má průměrně periodu oběhu Jupitera: J=11.862 a modrá křivka poloviční periodu konjunkcí Jupiter-Saturn: (J,S)/2 = 19.86/2 = 9.93 let.
Průchody Jupitera perihelem jsou poměrně pravidelné, ale odstupy konjuncí se - v důsledku pohybu planet na eliptických drahách - mění. Přesněji musíme tedy body funkcí počítat postupně - z aktuálních poloh planet. V každém okamžiku definujeme rozdíl longitud Jupitera a Saturna (dJS) a rozdíl longitud Jupitera a Jupiterova perihelu (dJp):
dJS = (Ls - Lj)/2;
dJp = Lj - Ljp;
|
Poté spočítáme hodnoty funkcí. Rozlišíme základní a alternativní funkce:
| Základní funkce | Alternativní funkce |
| var sJS = -Angles.Cosin(dJS); var sJp = -Angles.Cosin(dJp); | var sJS = Math.Abs(Angles.Sinus(dJS/2)); var sJp = Math.Abs(Angles.Sinus(dJp/2)); |

|

|
Skládání funkcí
Blízkost délek uvedených dvou period (9.93 a 11.86 let) umožňuje, že v některých obdobích mohou cykly běžet paralelně a vzájemně se posilovat. V jiných obdobích jeden z faktorů převažuje nad druhým, nebo se vzájemně kombinují.
Periody s délkami 9.93 let a 11.86 let tvoří rázy s periodou (9.93, 11.86) = 61 let a vnitřní periodou [J,S] = [9.93, 11.86] = 2*5.40 = 10.80 let. Zcela analogicky navrhl funkce E.W.Brown v roce 1900, který z pohybu Jupitera se Saturnem odvodil periodu (J,(J,S)/2) = 61 let. Opět jde o průměrnou periodu, ve skutečnosti délka kolísá podle poloh planet Jupiter a Saturn na eliptických drahách.
Na následujícím obrázku vidíme cca 60-ti letý interval 1885-1945. Prostřední části - tam kde se funkce dostávají do protifáze - říkáme "přechodné období".

Perioda slunečního cyklu 10.8 let bývá uváděna (často bez většího zdůvodnění) v různých teoriích, přestože neodpovídá periodě počítané ze známých cyklů, která vychází spíše o něco větší - okolo 11.05 let (přičemž ale zahrnuje v některých extrémech nejistotu - např. v cyklu okolo r.1797, jak jsme viděli výše...). Např. Peter Jakubowski vyčíslil v modelu Naturics z r.1998 délku periody na cca 10.81254 let. Z rezonance (3/2J-1/S) a Bretagnonových period vychází hodnota 10.807 let.
S dvojnásobnými periodami cyklů, tj. (J,S) = 19.859 let a 2J = 23.724 let pracuje ve své práci (z roku 2004) Milivoj A. Vukčevič. Zde je ale obtížné zdůvodnit význam periody 2J (jak jsme zmínili jinde - v pojednání o Obálkových funkcích).
Oběžné periody kentaurů Pholus a Nessus činí 91.79 let a 122.3 let. Tyto periody jsou přibližně v poměru 4:3, přičemž 91.79 let * 2/3 = 61.19 let a 122.3/2 = 61.15 let.
Délka cyklu
Dvojí délce primárních cyklů se zdá odpovídat i pozorovaná bipolarita délky cyklu sluneční aktivity - nejčastěji se vyskytující délky cyklu se rozdělují do 2 skupin (I. cca 10 let, II. cca 12 let).
První z period odvodil nejen Heinrich Schwabe (1789-1875) z evidence slunečních skvrn, ale také Karel Václev Zenger (1830-1908) ze známých výbuchů sopek. Na zhruba desetiletou periodu růyných jevů poukázali později i jiní pozorovatelé. Edward R.Dewey (1895–1978) se přiklání spíše k periodě nižší (9.6 let), T.W.Cole vyšší (10.45 let). Clément Juglar (1819-1905) určil trvání ekonomických cyklů na 10 let. V období 1780-1865 se ozývala sopka Etna v letech 1780, 1792-93, 1802, 1809, 1811-1812, 1819, 1832, 1843, 1852-53, 1865.
Průměrná perioda
Kdyby se účinky s průměrnými periodami (J,S)/2=9.93 a J=11.86 let rovnoměrně střídaly, vycházela by průměrná perioda slunečního cyklu cca 10.9 let. Povšimněme si však, že délka měřená mezi minimy je nejistá, protože minima mají různou hloubku i trvání (I.Usoskín) a že délka měřená mezi maximy je také nejistá, protože některá maxima mají více vrcholů (M.N.Gnevyšev). Navíc je mlhavý i průběh cyklů v obdobích, kdy aktivita téměř zaniká (Maunderovo minimum) nebo kdy se průběh aktivity ukazuje jinak než obvykle (okolo r.1797, I.Usoskin).
Vlastně je možné i vážně pochybovat o tom, jestli má o "průměrné periodě" smysl mluvit. Pokud běží paralelně dva cykly s blízkými periodami, může některý extrém patřit jednomu a jiný druhému cyklu a některé vrcholy mohou být výsledkem součtu obou cyklů, přičemž, o který případ právě půjde, může být těžké odhadnout. Přesný projev je jednak zkreslený našimi nepřesnými metodami pozorování a také může být ovlivněn vedlejšími vlivy, které v počátcích výstavby teorie nejsou známé.
Paradox jevů na Slunci
Podle jednoduché logiky by vyšší sluneční aktivita mohla být provázena většími slunečními erupcemi a následně také bouřemi a případně i jinými jevy na Zemi.
Ukazuje se však, že tomu tak není. Co se týče slunečních erupcí, jsou známé takové (např. erupce r.1941, erupce z let 1972-73, apod.), které se objevují mimo interval nejvyšší aktivity Slunce. A u geologických jevů jsou dokumentovány dokonce spíše případy opačné (např. erupce sopek v letech s dlouhodobě nižší aktivitou - viz chaotická období v teorii I.Charvátové).
Jinými slovy - s tím, co jsme nazvali negativními faktory - pro sluneční aktivitu, se často spojují pozitivní faktory - pro erupce na Slunci a geologické jevy (zemětřesení, erupce sopek) na Zemi. Postupně projdeme některé jednotlivé případy:
Sluneční bouře
Tři vybrané sluneční bouře v letech 1882-1941-2000 po sobě následují s intervalem cca 59-62 let. (Do stejného rastru zapadá i bouře r.1582.) Rok 1941 je poměrně daleko za vrcholem odpovídajícího cyklu (1937.4). To, co události spojuje, jsou poměrně přesná zarovnání obou výše uvedených funkcí v okolí let 1881-1941-2001.

17.-20.11.1882 |

1940 (březen) 17-19.9.1941 |

6.4.2000, 14.7.2000 (Bastille Day) 11.4.2001, 31.10.2003 (Halloween) |
| V-sun-EJS (1880) | EV-sun-JS (1940) | sun-VEJS (1999) |
Určitě se objevují bouře i mimo tento cca 60-ti letý cyklus. Někeré z nich však oět v zarovnání s funkcemi - např. bouři r.1770 (17.9.1770) najdeme o cca 10 let před přesným zarovnáním, minima funkcí se však za tuto dobu od sebe příliš nevzdálila.

Geologické jevy
Dne 16.2.1810, kdy se objevilo silné zemětřesení na Krétě. Toto zemětřesení bylo v letech 1811-1812 následováno katastrofálními zemětřeseními v New Madrid (16.12.1811, 23.1.1812 a 7.2.1812). Otřesy otočily tok řeky Mississippi proti proudu,... Následovalo zemětřesení v Santa Barbara/Ventura (21.12.1812). Sopka Tambora vybuchla v r.1815 (5.4.-10.4.2015). V období 1811-1815 se ozvalo ještě i několik dalších sopek - Sabrina (1811), Soufriere a Awu (1812), Mayon (1814), ...
V Čechách bylo větší zemětřesení zaregistrováno 14.1.1810 a později ještě v r.1813 a 1817.
| V r.1810 prochází Jupiter perihelem, v opozici k Uranu a Neptunu. (podobně jako r.1667, v době Maunderova minima). |

|

Tambora r.1815 |

Stromboli r.1822 (silné erupce) |

Cosequina r.1835 |

Krakatoa r.1883 |
Vedle sopky Cosequina (13.1.1835) vybuchly i sopky Osorno a Aconcagua. (zemětřesení bylo detekováno cca měsíc později, 20.2.1835). Sopka na Babujan Island se ozvala již r.1831.
Výbuchu sopky Krakatoa předcházel méně známý výbuch Tambory r.1880, v r.1881 bylo zemětřesení v Indii.
Další příklady synchronizací geologických událostí v návaznosti na extrémy zde uvedených funkcí najde čtenář na stránce:
Přírodní jevyPřechodná období
V přechodných obdobích (funkce v protifázi) se pozoruje poněkud jiný průběh přírodních jevů, než mimo ně. Výše uvedené velké erupce sopek z let 1815, 1822, 1835 a 1883 - stejně tak jako erupce sopky Pinatubo r.1991 se objevily mimo přechodná období (1785-1805, 1845-1865, 1905-1925, 1965-1985,...)
Sopky bývají řazeny do 3 typů (S,R,G), přičemž vrcholy aktivity sopek typu S a R byly určeny na okolí r.1930 a r 1950 (tj. mimo přechodná období), zatím sopky typu G měly v tomto období minimum, jejich maximum bylo cca r.1910, tj.uvnitř přechodného období.
Některá velká zemětřesení se pozorují na okrajích přechodných období, např. r.1783, r.1906, r.1964 (r.2023-26?).
Povodně nacházíme v přechodných obdobích - např. povodně v letech 1008 a 1068, nebo 1375 a 1434 - i mimo ně - např. novodobé povodně v období (1985-2025).
Více příkladů jevů pozorovaných během přechodných období je na stránce:
Přechodná obdobíOdeznívání přechodných období
Zaměřme se nyní na krátké intervaly za koncem přechodných období. Na mysli máme okolí let (v odstupech cca 59-61 let): 43, 104, 164, 224, 283, 342, 401-411, 471, 531, 590, 649, 709-719, 779, 838, 897, 947-957, 1007-1017, 1076, 1137, 1197, 1257, 1315-1325, 1384, 1445, 1503, 1563-1573, 1633, 1693, 1752, 1812, 1872, 1931, 1991, 2050, ...
Přechodná období se od sebe liší tvarem křivek, někdy proto dochází k posunům - extrémy nastávají o několik let dříve nebo později, než by se dalo čekat od přesné pravidelnosti 60-ti letých cyklů.
R.165 bylo zemětřesení v západní Evropě, r. 472 soptil Vesuv, okolo r.536 se k Vesuvu přidal Rabaul (Annus Horribilis). R. 781 Fudžisan, r.945-48 Paektu, r.1138 velké zemětřesení v syrském Aleppo, r.1257 sopka Samalas - patrně jedna z největších známých erupcí naší nedávné historie, 1315 sopka Mount Tarawera, 1444 erupce v Tyrrhénském moři, 1573 zemětřesení v Itálii, 1630-32 soptí Vesuv, 1693-94 Vesuv i Stromboli, 1755 velké zemětřesení v Lisabonu, 1811-12 zemětřesení v Kalifornii, 1815 sopka Tambora, 1991 sopka Pinatubo...
Planety v perihelech
Gravitační působení mezi Sluncem a planetou na eliptické dráze se mění. Zvláště výrazná může být tato proměnlivost u Jupitera, s periodou oběhu 11.86 let. Náznaky významu tohoto působení najdeme v práci I.Charvátové, P.Kalendy a v poslední době např. u francozských vědců V.Courtillot, F.Lopes, J.L.Le Mouël.
Podrobnější zkoumání korelace pohybu Jupitera na eliptické dráze a extrémy sluneční aktivity publikoval (koncem minulého století) Timo Niroma. Některé své závěry shrnul do stručných vět, z nichž za nejdůležitější považujeme: "The sunspot minima prefer an area around the Jovian perihelion." (Minima slunečních skvrn preferují oblast kolem Jupiteova perihelu).
Jupiter v perihelu
Povšimněme si některých záznamů o minimech aktivity v korelaci s polohou Jupitera v perihelu.
Pravidelnost s periodou opakování cca 165-180 let, tedy periodou opakování poloh vnějších planet, se zdá být zcela zjevná - byť se po r.1990 náhle vytrácí.
Cyklus Minimum aktivity J v perihelu -------------------------------------- -12 1610.8 1607,87 -11 1619.0 1619,73 -10 1634.0 1631,59 -9 1645.0 1643,46 -8 1655.0 1655,32 -7 1666.0 1667,18 -6 1679.5 1679,05 -5 1689.5 1690,91 |
Cyklus Minimum aktivity J v perihelu -------------------------------------- 3 1775.5 1773,95 4 1784.7 1785,81 5 1798.1 1797,68 6 1810.6 1809,54 7 1823.3 1821,40 8 1833.9 1833,27 9 1843.5 1845,13 10 1856.0 1856,99 11 1867.2 1868,86 12 1878.9 1880,72 |
Cyklus Minimum aktivity J v perihelu -------------------------------------- 20 1964.7 1963,76 21 1976.3 1975,62 22 1986.7 1987,49 |
Zajímá nás, která období "vypadla" a kde jsou přibližně jejich středy. V prvním období (1702-1762) dostaneme přiblině rok 1732, v druhém (1892-1952) - rok 1922. Pokud posuneme druhý střed (cca o jeden cyklus) zpět na r.1911, dostaneme:
J v perihelu ------------ 1702,77 1714,64 1726,50 1738,36 1750,22 1762,09 |
J v perihelu
------------
1892,58
1904,44
1916,31
1928,17
1940,03
1951,90
|
| r.1732 | r.1911 |

|

|
Obdobné opozice J-S,U-N najdeme také například poblíž let: 1057, 1216, 1395, 1573, resp. dále 2071, 2090, 2249
Popírání vlivu planet
Snažíme-li se prokázat vliv planet na Slunce, musíme také vyvrátit myšlenky těch, kteří tvrdí opak.
V roce 1913 G.F.Kronenberger (1885–1926) článek "Sunspot and the planets". V první části například uvádí rozdíly v polohách planet v letech 1788,1804 a 1837 v časech maximální aktivity a dále rozdíly v polohách planet v letech 1810,1843,1867 a 1878 v časech minimální aktivity. Ale právě tato vyjmenovaná data jeden společný jmenovatel mají. Jupiter procházel afelem (mimo jiné) v letech 1791.75, 1803.61 a 1839.2, zatímco perihelem prolétal v letech 1809.54, 1845.13 a 1880.72.
Zeslabování kvadratur?
Mluvíme - stejně jako v předchozích o kvadraturách Jupiter-Saturn, vrátíme se zpět k r.1797 a ptáme se, proč se zde (oproti jiným obdobím) maximum kvadratur neprojevilo? A proč se někdy maximum kvadratur skládá s aphelem Jupitera a někdy vystupuje samostatně?
Pokud porovnáme extrémy aktivity přesně na kvadratury, najdeme vždy období s vysokou korelací a pak období, kdy působení kvadratur není dostatečně silné a je překryto jinými vlivy. Tato období nás zajímají - vlastně jde v prvním přiblížení o období, kdy se kvadratury kryjí s minimy aktivity.
Přibližně jde o období (s přibližně stoletými odstupy):
1666-1698, 1755-1767, 1856-1887, 1964-1996.
Nabízí se myšlenka, zda nemůže být efekt kvadratur zeslabován v době, kdy Jupiter i Saturn prochází současně svými perihely. (Taková období skutečně existují - díky skutečnosti, že jsou přímky apsid Jupitera a Saturna přibližně na sebe kolmé...)
Roky které toto splňují rozdělíme do dvou skupin: I.1559, 1678, 1797, 1856, 1976 a II. 1618, 1737, 1916, 2035. První skupina (do které jsme zahrnuli i rok 1797) ukazuje na období kdy kvadraturami nedokážeme vysvětlit extrémy aktivity. V přechodných obdobích se extrémy aktivity objevují poblíž Jupiterova aphelu v letech: 1661, 1673, 1685 a později 1968.9, 1979.9.
Zbývá ale otázka, jak vysvětlit, proč totéž nenastává i pro roky druhé skupiny? Dochází někdy i naopak k "posilování kvadratur"? Poměrně vysoké maximum 1738.7 nastává během kvadratury Jupiter-Saturn, přestože jsou v r.1737 Jupiter i Saturn poblíž perihelu. Je tomu tak v době opozice Uran-Neptun, přičemž v r.1738 prochází opoziční přímkou Saturn. A analogická situace je vidět i pro maximum r. 1917.6.
Saturn v perihelu
IsPericentre(Ls, Lsp, 2);
1620,29 1649,94 1679,26 1708,91
1738,24 1767,89 1797,21 1826,78
1856,10 1885,67 1915,08 1944,57
1973,89 2003,46 2032,78 2062,35
|
Sledujme nyní na řadu let :1620, 1679, 1738, 1797, 1856, 1915, 1973, 2033, 2091 (tj. na data negativní interference dvou sledovaných cyklů). Doplněním o středy těchto intervalů (tj. o data pozitivní interference) dostaneme přibližně řadu: 1650,1709,1767,1826,1885,1944,2003,2062.
Porovnáním s pohybem Saturnu zjistíme, že v letech extrémní interference (pozitivní i negativní) cyklu Jupiterova afelu a kvadratur Jupiter-Saturn je (v námi sledovaném období) Saturn vždy v perihelu!
Uvedené pozorování zřejmě souvisí (ať už jako příčina nebo následek) s tím, že přímky apsid Jupitera a Saturnu jsou k sobě téměř kolmé.
Waldmeierův efekt
Tam, kde rozhodují o sluneční aktivitě kvadratury planet, připomíná blížení se ke kvadratuře otevírání pomyslného kohoutu, který spouští nějaký proud energie. A čím více se kohout otevře, tím rychleji se energie vybije. To je tzv.Waldmeierův efekt. Tedy čím je extrém aktivity vyšší - tím je aktuální cyklus kratší.
Pokud by byla prokázána souvislost mezi nižší aktivitou a větším vlivem Jupitera, pak jsou v obdobích nižší aktivity cykly automaticky delší, protože je perioda Jupitera delší, než poloviční perioda Jupiter-Saturn.
Minima v zarovnáních Jupiter-Saturn
V některých obdobích můžeme očekávat postup minim aktivity synchronně s konjunkcemi a opozicemi Jupiteru se Saturnem.
1633,31 1634.00
1643,04 1645.00
1653,76 1655.00
--------------
1713,31 1712.00
1723,08 1723.50
1732,32 1734.00
1742,67 1745.00
--------------
|
1811,83 1810.60
1821,69 1823.30
1832,45 1833.90
1842,18 1843.50
--------------
1901,73 1901.70
1911,30 1913.60
1921,61 1923.60
--------------
|
2020,83
2030,69 ?
2040,91 ?
|
Kvadratury Uran-Neptun
V následujících schematech svírají longitudy planet Uran a Neptun přibližně pravý úhel, tj. jsou v kvadratuře. Přitom těmto postavením předcházely (v předstihu 1-2 roky) i kvadratury planet Jupiter a Saturn (1778.4-1777.4=1.0 let, 1947.50-1946.47=1.03 let, 1957.90-1956.17=1.73 let):
Následující tři obrázky představují pozici planet v čase největších extrémů (maxim) sluneční aktivity posledních tří století....
23.5.1778
 30.6.1947
30.6.1947
 22.11.1957
22.11.1957

Pět z deseti největších slunečních skvrn let 1874-2014 bylo pozorováno v letech 1946-1951. (Pozice z let 1778 a 1957 jsou obdobné, v souladu s 178-180-ti letý cyklem poloh vnějších planet).
Postupný nárůst aktivity (červeně) v první polovině 20-tého století, může být zjednodušeně modelován kombinací tří vlivů:
- cyklu Jupitera (černě)
- cyklu Jupiter-Saturn (bledě modře)
- cyklus Uran-Neptun (modře)

Ne vždy však vystupuje kvadratura Uran-Neptun takto do popředí.
Kvadratura r.1698 zaniká v čase Maunderova minima a Slunce se
z minima probouzí až ještě cca o 10 let později.

Gleissbergova maxima
Gleissberg(1965)
| Pořadí | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Gleissberg | 360 | 440 | 510 | 575 | 665 | 755 | 840 | 920 | 990 | 1115 | 1185 | 1250 |
| Kvadratura U#N | 322 | 409 | 495 | 581 | 667 | 754 | 839 | 926 | 1011 | 1098 | 1183 | 1270 |
| Pořadí | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Gleissberg | 1305 | 1375 | 1455 | 1545 | 1605 | 1715 | 1765 | 1840 | 1955 | |||
| Kvadratura U#N | 1355 | 1441 | 1527 | 1613 | 1698 | 1784 | 1869 | 1955 | 2041 | |||
V obdobích poblíž posledních dvou kvadratur (1869, 1955) se pozorují vyšší amplitudy slunečních cyklů (v letech 1840-1880,1930-1970), zatímco v meziobdobí 1880-1930 aplitudy nižší. (Přitom podle pozorování ve Velké Británii byla v obdobích kvadratur teplota vzduchu ve fázi s cykly aktivity, zatímco v meziobdobí nikoliv).
Maunderovo minimum
Úplné zklidnění Slunce během tzv. Maunderova minima je záhadou. Odvodit ho jen z konjunkce Uran-Neptun roku 1650 a s ní souvisejícího retrográdního pohybu Slunce není možné, při každé konjunkci Uran-Neptun taková minima nenastávají.
Za Maunderovo minimum se často považuje období až po roce 1650, ale existují indicie, že na Slunci došlo k některým významným změnám již dříve - Slunce začalo rychleji rotovat. V letech 1611-1613 trvala jedna otočka Slunce na rovníku 26.163 dní, v letech 1625-1626 24.913 dní a v letech 1642-1644 24.3 dne. V následujících stoletích se pak Slunce opět postupně zpomalilo.
Ohledně výšky maxima byl ale pozorován výraznější pokles až skutečně po r.1650. Výška maxima r.1625 byla ještě cca 115, výška maxima r.1639 cca 100. Maxima let 1650,1661,1673,1685 a 1694 nevybočují z intervalu hodnot 10-45 a nárůst nastal až po r.1700 - s výškami u maxima r.1705 cca 70, u maxima r.1718 cca 90 a u maxima r.1727 s výškou cca 140.
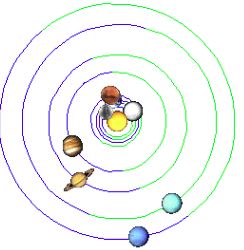
|
Po konjunkci z r.1650 se úhel mezi planetami Uran a Neptun postupně rozevírá, roku 1662 (obrázek) se pohybují přibližně na longitudě Jupiterova perihelu, následovány Jupiterem a Saturnem. |
| Okolo r.1665 (obrázek) je Saturn v afelu. Jupiter je uvnitř úhlu Uran-Neptun a blíží se k perihelu r.1667. V r. 1667 je již mezi Uran a Neptun vklíněn Saturn, přičemž síla od Jupitera neklesá, protože se přesunul do perihelu. |

|
| Než se konjunkce Uranu s Neptunem pozorovaná po roce 1662 postupně rozpojí musí kolem ní Jupiter i Saturn několikrát projít (Jupiter 4x, Saturn 2x), zde je uskupení na počátku roku 1705: |
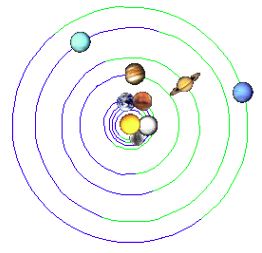
|
Období 1600-1630 a 1660-1690 byla přechodná. Nějaký vliv ale musel způsobit výrazné zeslabení obou funkcí v protifázi.
Nízkým maximům v letech v letech 1650,1661,1673,1685,1694 a 1705. odpovídají přibližně Jupiterovy průchody afelem 1649.39, 1661.25, 1673.11, 1684.98, 1696.84 a 1708.7:

Situace okolo r.2000
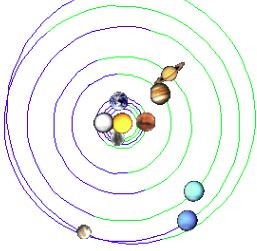
|
Rozložení planet v r.2000 připomíná rozložení z r.1662, zde jsou však již Jupiter a Saturn za linií konjunkce Uran-Neptun a proto se podobný vývoj jako po r.1662 nedal očekávat. |
A také - nejbližší přechodná období k roku 2000 jsou 1960-1990, 2020-2050, tedy r.2000 do nich nezasahuje.
Carringtonův extrém
Za Carringtonův extrém označujeme maximum aktivity roku 1860.1 spojené s protonovou událostí a sluneční velkou bouří 1.9.1859. Velké sluneční skvrny byly pozorovány v letech 1859-60. V souvislosti s tímto extrémem bývá zmiňována také polární záře 14.12.1862. Někdy se mluví také o druhém maximu r.1864(?).
V čase extrému r.1860 není žádný ze dvou hlavních vlivů, které uvažujeme, extrémní. Kvadratura Jupiter-Saturn nastala již v r. 1857, Jupiter byl afelu až v r.1862 a přesná kvadratura Uran-Neptun až v r.1869.
Rok 1857 je 60 let po dříve sledovaném roce 1797. A rok 1858.5 (Wolfův cyklus č.10) je přibližně středem mezi extrémy r.1727.5 (Wolfův cyklus č.-2) a r.1989.6 (Wolfův cyklus č.22) - s odstupem mezi těmito daty cca 131 let.
| Carrington proton event, solar superstorm, 1.9.1859 | The Civil War Aurora, Aurora Borealis, 14.12.1862 |
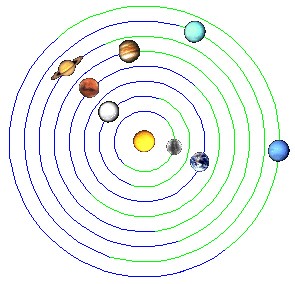
|

|
Rozdíl mezi daty 1200 dní, tj. přibližně 2*(V,E) (= 2*584 dní = 1168 dní). (Navyšuje opozice Venuše-Země působení konjunkce Jupiter-Saturn?!)
Násobná maxima
Za roky s dvojitými nebo vícenásobnými maximy se uvádí např. 1829,1894,1906,1928. Maxima 1906,1928 jsou na okrajích přechodného období:

Problém s objasněním extrémů
Problém prvního Wolfova cyklu
Uváděné maximum r.1761 nijak nekoresponduje s výše uvedenými křivkami, v blízkosti roku 1761 je Jupiter poblíž perihelu a v konjunkci se Saturnem (a Uranem). I přesto je zřejmě určené správně - obdobná situace nastala v nedávné minulosti znovu, v maximu r.1989-90, jak uvidíme v následujícím odstavci.
Pozorování skvrn na Slunci v letech 1761-1776 prováděl Christian Horrebow (1718-1776), záznamy z let 1762-1763 se však nedochovaly.
Požáry r.1871
Podobná situace se objevuje cca o 109 let později, v roce 1870. I zde je maximum aktivity s Jupiterem poblíž perihelu a v konjunkci se Saturnem a tentokrát v blízkosti kvadratury Uran-Neptun (1869). V Americe bylo po r.1870 extrémní sucho, v jeho důsledku se 2 požáry (požár v Peshtigo a požár v Chicagu), které vznikly z ne zcela objasněných příčinr stejný den 8.10.1871, rozšířily do několika států.
Poloha planet 8.10.1871 připomíná polohu v době Carringtonovy sluneční bouře 1.9.1859. Jupiter poblíž konjunkce s Uranem je na cestě ke svému afelu. Neptun je k těmto planetám přibližně v kvadratuře a Saturn v r.1859 v konjunkci a v r.1871 v opozici s Jupiterem. Shoda je i v tom, že v obou případech je Země v konjunkci s Neptunem a Mars se Saturnem. A Venuše je v r.1859 v opozici a v r.1871 v konjunkci se Zemí.
Problém konce 20-tého století
V jednom z úvodních odstavců o konjunkcích planet a jejich vlivu na sluneční aktivitu jsme zmínili minima v okolí let 1306 a 1810. Až tak jednoduše, se však příčinná souvislost nemá. O 179 let později, v roce 1989- při velmi podobné poloze planet - nastalo vysoké maximum aktivity.
| Minimum 1810 | Maximum 1989 |

|

|
Predikce sluneční aktivity konce a přelomu 20-tého století (v tabulce viz predikce podle Waldmeiera a Schove) selhaly - extrémy očekávané cca na r.1993, a r.2004 se objevily o cca 4 roky dříve.
Vysoká aktivita v letech 1989-90 (druhá nejvyšší úroveň od dob Galileových pozorování) následuje cca 262 let po maximu r.1727, 229 let po výše zmíněném maximu r.1761 a 131 let po Carringtonově maximu r.1859. Co ji způsobilo je záhadou, stejně jako původ potenciálního 130-ti letého cyklu. Roky 1761 a 1989 mírně připomíná Pluto (to prochází perihelem v letech 997, 1245, 1493, 1741, 1989 a 2237).
| Cyklus | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Waldmeier, 1966 | 1968.9 | 1981.2 | 1993.0 | 2004.0 | |||
| Schove, cca 1950 | 1958.5 | 1972.5 | 1984.5 | 1994.5 | 2004.5 | 2014.5 | 2025.5 |
| Skutečnost | 1957.9 | 1968.9 | 1979.9 | 1989.6 | 2000.3 | 2014.0 |
Podle funkcí, které zde sledujeme, vychází extrémy v tomto období také jinak, než ve skutečnosti:

Kromě toho bylo také pozorováno, že:
- Bouře na Slunci v srpnu 1972 (největší rozměr 4.8.1972) byla silnější než bouře v r.1959.
- Nejsilnější erupci 24. cyklu byla (X93) z 6.9.2017.
Nejvyšší aktivita ve 20-tém století (včetně velkého počtu slunečních bouří) je spojena s roky 1957-1960 a 1989-1991. Saturn byl v afelu r.1959.6 a 1988.7, Jupiter procházel afelem r.1957.8 a v r.1993.4 (v roce 1987.5 byl ještě v perihelu). Průměry odpovídajících extrémů činí 1958.7 a 1991.1 a jejich odchylka od extrémů z pozorování (maxima: 1957.9, 1989.6, mediány: 1958.6, 1990.7) je v řádu jednoho roku.
Planeta X
Jednou z mála možností, jak nezahodit celý, zde předkládaný koncept, je úvaha o dalším tělese nebo tělesech za hranicí sluneční soustavy, jak ji dnes známe.
Planeta s periodou cca 390 let
Úvahu o tom, jaké vztahy by přinášela do Sluneční soustavy planeta s periodou cca 390 let najde čtenář na této stránce:
Planeta XNávrh vycházel z myšlenky, že by Planeta X neměla - v synodických periodách s ostatními tělesy - narušovat cyklus s periodou B=427 let, resp. 2B=854 let, který se ve Sluneční soustavě pozoruje. Zároveň měla vnést do systému i periodu cca 109 let (3 Brucknerovy periody), která je ve Sluneční soustavě a klimatu pozorována a pro níž nemáme jiné vhodné vysvětlení. V tomto návrhu je 109 letá perioda synodickou periodou (periodou konjunkcí) planety X s planetou Uran.
Planeta s periodou cca 575 let
Úvahu o planetě s periodou cca 575 let najde čtenář zde:
Obálkové funkcePokud uvažujeme, že perioda cca 105-125 let, kterou se zdá být Sluneční aktivita - v porovnání s během známých planet - narušena je periodou kvadratur nějakých dvou těles, pak skutečná synodická perioda těles musí být dvojnásobná, řekněme přibližně 2*115 = 230 let. Takovou synodickou periodu by měla planeta Neptun s planetou X tehdy, pokud by X měla periodu cca 575 let.
Perioda 575 let se pozoruje v pohybech některých planet a tvoří s planetou Uran synodickou periodu cca 98 let, která připomíná cyklus, s jakým jsou narušovány fáze Slunečních cyklů - specielně při porovnávání s kvadraturami planet Jupiter a Saturn.
Predikce
Jupiterův efekt
V knize Jupiterův efekt (1974) předpovídali autoři (John R.Gribbin a S.Plagemann) ze zarovnání planet velké zemětřesení na den 10.3.1982.

Neúspěch této předpovědi bývá někdy připomínán, když se objeví jiné předpovědi, např.když bylo na období okolo roku 2020 predikováno zvýšení geologické činnosti. Mezi roky 1982 a 2020 však pozorujeme výrazný rozdíl:

Predikce bouří
Výše uvedené sluneční bouře 1882-1941-2000 se přibližně kryjí s extrémy slapového působení planet na Slunce - v různých kombinacích zarovnání těles Jupiter, Saturn, Země a Venuše. Působení planet Venuše a Země je však (vzhledem k malým periodám) zřejmě podružné. Za hlavní faktory považujeme konjunkce Jupiter-Saturn (modrá křivka) a průchody Jupitera perihelem (zřejmé podle černé křivky). Odtud roky možných budoucích bouří:

Známé je, že pokud na Slunci zůstává větší aktivní oblast resp.větší sluneční skvrna delší dobu (jako např. v letech 1840-41 jedna ze skvrn 18 měsíců), dá se očekávat opakování geomagnetických bouří na Zemi s periodou rotace Slunce - tj. z pohledu ze Země cca 27 dní.
Predikce ledových dob
Obdobná rozložení planet najdeme před naším letopočtem např. v letech 922 BC, 743 BC (Homérovo minimum cca 770 BC), 245 BC a 67 BC. Počínaje začátkem letopočtu najdeme obdobný obrázek po r.113 (kdy tabulky sestavené Justinem Schove ukazují na velmi nízkou sluneční činnost s nejistými extrémy). Další podobnou polohu najdeme až v r.1483 (období 1460-1550 je tzv.Sporerovo minimum), resp. pak v námi pozorovaném r.1662 (tzv. Maunderovo minimum v období 1645-1715).
Za uvedených předpokladů můžeme pak predikovat malé doby ledové přibližně na období po r.2158, 2337 a potenciálně 2517. Tyto předpovědi poklesu aktivity odpovídají výsledkům z pozorování tzv. překrývání cyklů (zde byla odhadem z grafu stanovena minima na okolí let 2150, 2350 a 2500). O Překrývání cyklů je pojednáno na stránce:
Babylónská perioda