Sluneční aktivita - Rezonance
A.M.Molchanov| A.M.Molchanov , [molčanov] -, ruský matematik. Věnoval se matematickému modelování v biologii, ekologii, genetice apod. Předpokladal existenci rezonanční struktury sluneční soustavy. Vývoj drah planet vede podle něj k rezonancím a orbitálním periodám v poměru malých celých čísel. Nvrhl některé vztahy jak pro sluneční soustavu, tak i pro systémy měsíců Jupitera a Saturnu. |
Rezonance orbitálních period
Úvod
Tři Jupiterovy a tři Uranovy měsíce respektují tzv.Laplaceovu rezonanci, která omezuje možnost společných konjunkci. Jde o určitý princip minimální interakce - který zajišťuje rovnováhu.
Rezonance nemá tedy obecně jen podobu rušícího elementu (který dokáže rozbíjet předměty, bortit mosty apod.), ale také může být věcí, která zajistí synchronizaci a stabilitu.
U měsíců Jupitera/Uranu je jednoduchý argument - jsou synchronizovány díky slapovým silám. Podle A.M.Molchanova (1965,1968) však tělesa mohou být vedena k synchronizaci i při působení velmi slabých sil. Molchanov uvažuje o "malých disipativních sílách", v některých novějších teoriích byly navrženy i jiné hypotézy (M. B. Gubaidullin, 2015, viz také N. Scafetta, 2013).
Podle chování měsíců Jupitera/Uranu se nabízí zobecnění - vícenásobné konjunkce těles nejsou ve Sluneční soustavě žádoucí - je tendence aby se objevovali jen minimálně, aby nenastávaly přesně nebo aby byly nějak vyváženy.
Malá (slapová) působení mohou umocňovat přirozenou oscilaci sluneční atmosféry a působit velké změny.
Rezonance vnitřních planet
J.J.Condon a R.R.Schmidt v práci (1975) odvozují rezonanční vztah ve tvaru Lt = 3*Lv -5 *Le + 2*Lj, kde Lv,Le a Lj jsou longitudy Venuše, Země a Jupitera.
Z porovnání synodických period planet je možné vysledovat,
že ((E,J)/5 ,(V,J)/3) = 2∙W. Pak 1/(2W) = 3/V-5/E+2/J, a 2W = 22.13505 let,
tj. W = 11.06753 let.
Maxima sluneční aktivity nastávají přibližně, když (pro longitudy Venuše,
Země a Jupitera) platí:
3LV - 5LE + 2LJ = kπ
To ale neplatí vždy...
Wilsonovo upřesnění
Odtud odvozujeme:
41LV - 69LE + 28LJ = kπ
Z poměrů 41/69 vychází perioda 22.386 let (K.Takahashi, 1967).Mayové
Za 2W=22.3855 let postoupí J o 40.6 dg zpět, tj.pozorujeme-li soustavu s periodou 2W, nabudeme dojmu, že Jupiter obíhá proti směru s periodou cca 198.4 let. Kdyby se takto skutečně pohyboval, potkal by se se Saturnem každých 25.65 let tj.4*I nebo 3*Y, kde I je perioda vnitřních planet = 6.4 let a Y je 8.54 let. Rozdíl 25.65 a 22.39 let činí 3.26 let. (52 Tun/ 72 Almanac Cycle 18720 d, Calendar Round 52 Haab/73 Almanac Cycle 18980 d).
Molchanovovy rezonance
Molchanovovy rezonance: [M,-V,-E/2,-R] [V, -R/3, -S] [E,-R/2, J,-S, U], [R,J/6,-U/2] [J/2,-S/5] [J,-U/7],[U,-N/2], [U,-P/3] (plus jejich lineární kombinace...) /p>
Rezonance s periodou H
V opakování klimatických období se objevuje tzv. halštatský cyklus (H=2300 let), který koreluje s rezonancí orbitálních period vnějších planet.
Rozdíl periody 2403.05 let a 2224.10 let (se součtem 4627 let) je 178.95 let, ale společným dělitelem je spíše perioda 185.1 let (+-0.2 let), která může být modelována rezonancí 1/J-3/S+2/N (resp.((U,N),H)).
Vyvažování Jupitera
Vliv NeptunaOsová perioda Jupiter-Neptun, [J,N] = 22.13075 let = 2∙11.06538 let koinciduje s periodou Sluneční aktivity.
Někteří autoři (Ray Tomes,…) spojují Sluneční aktivitu s těmito dvěma tělesy (Jupiter, Neptun).
(V kombinaci s rezonancí vnitřních planet by vycházelo 6/V-10/E+3/J-1/N = 0, tj.nestabilní rezonance).
Význam Jupitera je (vzhledem k hmotnosti) jasný. Neptun může nabývat svého vlivu díky vzdálenosti od Slunce,
viz například hodnoty M*r2 (moment setrvačnosti):
| M [1024 kg] | a [109 m] | M*a2 [1039kg*m²] | |
| Jupiter | 1899,0 | 778,6 | 1151,2 |
| Saturn | 568,0 | 1433,5 | 1167,2 |
| Uran | 86,8 | 2872,5 | 716,2 |
| Neptun | 102,0 | 4495,1 | 2061,0. |
Rezonance
Také perioda rezonance 1/W = 1/J + 1/U – 1/N koreluje hodnotou W = 11.094 let s průměrnou periodou slunečního cyklu. Přepíšeme ji na tvar stabilní rezonance: 1/W - 1/J + 1/N - 1/U = 0.
Rezonanční maxima nastávají, když (pro longitudy Jupitera, Jupiterova perihelu, Uranu a Neptuna) platí:
Lj – Ljp + Lu - Ln = π+2kπ
Rezonanční minima nastávají, když (pro longitudy Jupitera, Jupiterova perihelu, Uranu a Neptuna) platí:
Lj – Ljp + Lu - Ln = 2kπ
Tato rezonance váže periodu sluneční aktivity W s periodami planet Jupiter, Neptun, Uran. Saturn je zde zdánlivě mimo hru - je však vázán rezonancí vnějších planet k Jupiterovu perihelu (viz Vliv Jupitera)!?
Znázornění vztahu
Rezonance vzniká ze součtu dvou úhlů ∆J + ∆UN, kde:
- ∆J = Lj-Ljp (Jupiter vzhledem k svému přísluní)
- ∆UN = Lu-Ln (Uran vzhledem k Neptunu).
| n | Mo | ∆J | ∆UN | n | Mo | ∆J | ∆UN | n | Mo | ∆J | ∆UN | n | Mo | ∆J | ∆UN | |||
| -30 | 1416,7 | 316 | 224 | -14 | 1594,4 | 306 | 234 | 2 | 1772,0 | 296 | 244 | 18 | 1949,5 | 283 | 257 | |||
| -29 | 1428,0 | 296 | 244 | -13 | 1605,6 | 286 | 254 | 3 | 1783,1 | 273 | 267 | 19 | 1960,5 | 257 | 283 | |||
| -28 | 1439,2 | 275 | 265 | -12 | 1616,6 | 262 | 278 | 4 | 1794,1 | 246 | 294 | 20 | 1971,4 | 229 | 311 | |||
| -27 | 1450,2 | 251 | 289 | -11 | 1627,6 | 235 | 305 | 5 | 1805,0 | 218 | 322 | 21 | 1982,4 | 203 | 337 | |||
| -26 | 1461,2 | 224 | 316 | -10 | 1638,5 | 207 | 333 | 6 | 1815,9 | 192 | 348 | 22 | 1993,4 | 180 | 0 | |||
| -25 | 1472,0 | 197 | 343 | -9 | 1649,4 | 182 | 358 | 7 | 1826,9 | 168 | 312 | 23 | 2004,5 | 159 | 21 | |||
| -24 | 1483,0 | 172 | 8 | -8 | 1660,5 | 160 | 20 | 8 | 1838,1 | 149 | 31 | 24 | 2015,7 | 140 | 40 | |||
| -23 | 1494,1 | 150 | 30 | -7 | 1671,6 | 140 | 40 | 9 | 1849,3 | 130 | 50 | 25 | 2026,8 | 120 | 60 | |||
| -22 | 1505,3 | 130 | 50 | -6 | 1682,8 | 120 | 60 | 10 | 1860,4 | 109 | 71 | 26 | 2037,9 | 96 | 84 | |||
| -21 | 1516,4 | 110 | 70 | -5 | 1694,0 | 99 | 81 | 11 | 1871,5 | 85 | 95 | 27 | 2049,0 | 70 | 110 | |||
| -20 | 1527,5 | 88 | 92 | -4 | 1705,0 | 74 | 106 | 12 | 1882,5 | 58 | 122 | 28 | 2060,0 | 42 | 137 | |||
| -19 | 1538,6 | 63 | 117 | -3 | 1716,0 | 47 | 133 | 13 | 1893,5 | 31 | 149 | 29 | 2071,1 | 18 | 162 | |||
| -18 | 1549,6 | 36 | 144 | -2 | 1727,1 | 21 | 159 | 14 | 1904,6 | 7 | 173 | 30 | 2082,3 | 356 | 184 | |||
| -17 | 1560,7 | 10 | 170 | -1 | 1738,2 | 357 | 183 | 15 | 1915,9 | 346 | 194 | 31 | 2093,6 | 336 | 204 | |||
| -16 | 1571,9 | 346 | 194 | 0 | 1749,5 | 336 | 204 | 16 | 1927,2 | 326 | 213 | 32 | 2104,8 | 316 | 224 | |||
| -15 | 1583,7 | 326 | 214 | 1 | 1760,8 | 316 | 224 | 17 | 1938,4 | 306 | 234 | 33 | 2116 | 294 | 246 |
Pozorovaná maxima jsou (podle směrů os) rozdělena do 4 různých typů,
viz např. I.1727.5 (140.0), II.1870.6 (140.5), III. 1989.6 (150.1), IV. 1957.9 (201.3) :

The relation of U-N angle on one side and J-Jp angle on other side seems to be rather incomprehensible. But possibly – it is not random: U-N angle can have some influence on stability of the motion of other planets around barycentre (and also on long-term solar activity). And distance of Jupiter from its perihelion can be something like counterweight against it. The real distance of Jupiter and the Sun can also have some influence on "actual" stability of the Solar system...
Porovnání extrémů - maxima
V následujícím přehledu jsou porovnána maxima:
- maximum Sluneční aktivity MS
- maximum Woodovy rezonance vnitřních planet MI: 3LV - 5LE + 2LJ = kπ
- maximum rezonance vyvažování vnějších planet MO: LJ - LN + LU = LJP + π (+2kπ)
- maximum rezonance geometrických os MA: (LJ - LS) + (LN - LU) = kπ/2
1500-1650
| N | WS | WI | WO | WA | WI-WS | Wo-WS | Wo-WI | |
| -23 | 1492 | 1494,6 | 1494,1 | 1490,4 | 2,6 | 2,1 | -0,5 | |
| -22 | 1505 | 1505,8 | 1505,2 | 1501,6 | 0,8 | 0,2 | -0,6 | |
| -21 | 1519,0 | 1517,3 | 1516,4 | 1513,1 | -1,7 | -2,6 | -0,9 | |
| -20 | 1528,0 | 1527,5 | 1527,5 | 1523,7 | -0,5 | -0,5 | 0,0 | |
| -19 | 1539,0 | 1539,1 | 1538,6 | 1535,6 | 0,1 | -0,4 | -0,5 | |
| -18 | 1548,0 | 1549,6 | 1549,6 | 1546,9 | 1,6 | 1,6 | 0,0 | P-maximum |
| -17 | 1558,0 | 1560,8 | 1560,7 | 1558,1 | 2,8 | 2,7 | -0,1 | |
| -16 | 1572,0 | 1572,5 | 1571,9 | 1570,1 | 0,5 | -0,1 | -0,6 | |
| -15 | 1581,0 | 1583,6 | 1583,7 | 1580,4 | 2,6 | 2,7 | 0,1 | |
| -14 | 1591,0 | 1594,6 | 1594,4 | 1591,7 | 3,6 | 3,4 | -0,2 | |
| -13 | 1604,0 | 1606,2 | 1605,6 | 1602,8 | 2,2 | 1,6 | -0,6 | 1607 - Kepler's spot |
| -12 | 1615,5 | 1616,8 | 1613,1 | 1613,0 | 1,3 | 1,1 | -0,2 |
1618 - Simon Mair's (Marius) spots |
| -11 | 1626,0 | 1627,8 | 1627,6 | 1625,3 | 1,8 | 1,6 | -0,2 | |
| -10 | 1639,5 | 1638,8 | 1638,5 | 1636,3 | -0,7 | -1,0 | -0,3 |
| n | WS | WI | WO | WA | WI-WS | WO-WS | WO-WI | |
| -9 | 1649,0 | 1649,9 | 1649,4 | 1647,5 | 0,9 | 0,4 | -0,5 | |
| -8 | 1660,0 | 1660,8 | 1660,5 | 1659,2 | 0,8 | 0,5 | -0,3 | 1660 - Hevelius spots, 1661 - Boyle and Picard sunspot group |
| -7 | 1675,0 | 1672,2 | 1671,6 | 1669,5 | -2,8 | -3,4 | -0,6 | 1671 (August) - Pickard spot, Hevelius spot, 1676 - Pickard extreme, Maunder |
| -6 | 1685,0 | 1682,5 | 1682,8 | 1681,0 | -2,5 | -2,2 | 0,3 | 1684 - Pickard extreme, Cassini, Kirch |
| -5 | 1693,0 | 1693,5 | 1694,0 | 1692,2 | 0,5 | 1,0 | 0,5 | |
| -4 | 1705,5 | 1705,2 | 1705,0 | 1703,1 | -0,3 | -0,5 | -0,2 | |
| -3 | 1718,2 | 1716,0 | 1716,0 | 1715,2 | -2,2 | -2,2 | 0,0 | 1716 - visible aurora, 1714-15 - P-maximum, end of Maunder period |
| -2 | 1727,5 | 1727,4 | 1727,1 | 1726,3 | -0,1 | -0,4 | -0,3 | |
| -1 | 1738,7 | 1738,5 | 1738,2 | 1737,8 | -0,2 | -0,5 | -0,3 | |
| 0 | 1750,3 | 1750,1 | 1749,5 | 1749,2 | -0,2 | -0,8 | -0,6 | 1752 - second maximum |
| 1 | 1761,5 | 1761,3 | 1760,8 | 1759,7 | -0,2 | -0,7 | -0,5 | |
| 2 | 1769,7 | 1771,8 | 1772,0 | 1771,4 | 2,1 | 2,3 | 0,2 | 1774 - second maximum |
| 3 | 1778,4 | 1782,8 | 1783,1 | 1782,3 | 4,4 | 4,7 | 0,3 | |
| 4 | 1788,1 | 1794,5 | 1794,1 | 1793,4 | 6,4 | 6,0 | -0,4 |
| n | WS | WI | WO | WA | WI-WS | WO-WS | Wo-WI | |
| 5 | 1805,2 | 1805,5 | 1805,0 | 1805,7 | 0,3 | -0,2 | -0,5 | |
| 6 | 1816,4 | 1815,6 | 1815,9 | 1816,3 | -0,8 | -0,5 | 0,3 | |
| 7 | 1829,9 | 1827,2 | 1826,9 | 1827,7 | -2,7 | -3,0 | -0,3 | |
| 8 | 1837,2 | 1838,3 | 1838,1 | 1838,7 | 1,1 | 0,9 | -0,2 | |
| 9 | 1848,1 | 1849,2 | 1849,3 | 1848,9 | 1,1 | 1,2 | 0,1 | 1847-48 - Giant sunspots |
| 10 | 1860,1 | 1860,2 | 1860,4 | 1860,7 | 0,1 | 0,3 | 0,2 | 1859 - proton event (Carrington), 1864 - second maximum, 1859-60 - Giant sunspots |
| 11 | 1870,6 | 1871,3 | 1871,5 | 1871,6 | 0,7 | 0,9 | 0,2 | 1870-71 - Giant sunspots, 1870 - proton event (Young) |
| 12 | 1883,9 | 1881,7 | 1882,5 | 1882,9 | -2,2 | -1,6 | -0,8 | 1882 - P-maximum, 1882 - Giant sunspot, 1882 - proton events (Maunder) |
| 13 | 1894,1 | 1893,5 | 1893,5 | 1894,9 | -0,6 | -0,6 | 0,0 | 1892-93 - Giant sunspots, 1892 - proton events (Rudeaux) |
| 14 | 1907,0 | 1904,5 | 1904,7 | 1905,7 | -2,5 | -2,3 | -0,2 | 1905,07,08 - Giant sunspots, 1908 - proton event |
| 15 | 1917,6 | 1916,1 | 1915,9 | 1917,3 | -1,5 | -1,7 | -0,2 | 1917 - Giant sunspot, 1917 - proton event |
| 16 | 1928,4 | 1926,7 | 1927,2 | 1928,4 | -1,7 | -1,2 | -0,5 | 1926,29 - Giant sunspots, 1926 - proton event |
| 17 | 1937,4 | 1937,9 | 1938,4 | 1939,1 | 0,5 | 1,0 | 0,5 | 1935,37-42 - Giant sunspots, 1938 - proton event |
| 18 | 1947,5 | 1949,5 | 1949,6 | 1951,1 | 2,0 | 2,1 | 0,1 | 1946 - proton event, 1949 - proton event |
| n | WS | WI | WO | WA | WI-WS | WO-WS | WO-WI | |
| 19 | 1957,9 | 1960,5 | 1960,5 | 1962,1 | 2,6 | 2,6 | 0,0 | 1958 - the highest level since Galileo's observations (1610), 1956,59-61 - proton events |
| 20 | 1968,9 | 1972,2 | 1971,4 | 1973,8 | 3,3 | 2,5 | -0,8 | 1969 - proton event, 1972 - extreme flare, 1972 - second maximum |
| 21 | 1979,9 | 1983,2 | 1982,4 | 1985,5 | 3,3 | 2,5 | -0,8 | 1981 - extreme flare |
| 22 | 1989,6 | 1993,2 | 1993,4 | 1996,1 | 3,6 | 3,8 | 0,2 | 1990 - the second highest level since Galileo's observations (1610) |
| 23 | 2000,5 | 2004,3 | 2004,6 | 2007,8 | 3,8 | 4,1 | 0,3 | |
| 24 | ? | 2015,3 | 2015,7 | 2018,3 | ? | ? | 0,4 | |
| 25 | ? | 2026,1 | 2026,8 | 2028,9 | ? | ? | 0,7 | |
| 26 | ? | 2036,6 | 2037,9 | 2040,9 | ? | ? | 1,3 | |
| 27 | ? | 2048,1 | 2049,0 | 2051,5 | ? | ? | 0,9 | 2050-51 - P-maximum |
| 28 | ? | 2059,5 | 2060,0 | 2063,4 | ? | ? | 0,5 | |
| 29 | ? | 2070,6 | 2071,1 | 2074,7 | ? | ? | 0,5 |
Následné úvahy
Pravidelnosti
Teoretické extrémy (maxima i minima) sluneční aktivity probíhají přibližně se stejnou periodou jako skutečné extrémy. Největší rozdíly v maximech jsou pozorovány v letech 1583-1606, 1675-1685, 1778- 1788, 1829, 1958-2000. Největší rozdíly v minimech jsou pozorovány v letech 1553,1619, 1784, 1902-1924,1996.
Justin Flynn si povšiml určité pravidelnosti těchto odchylek (osobní komunikace).
Podívejme se na následující graf:
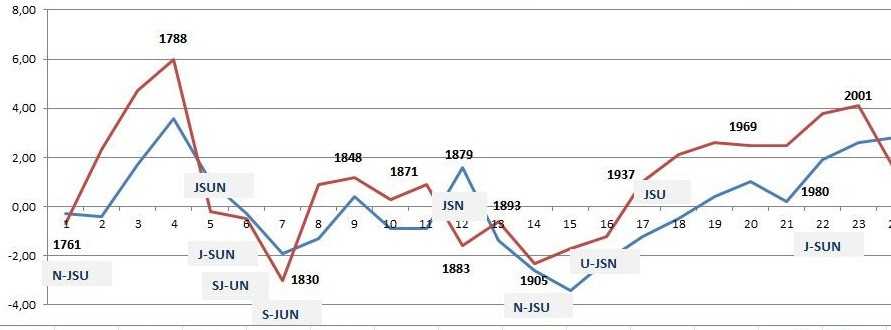
Pravidlo střídání odchylek
Rozdělme konjunkční cyklus Uran-Neptun na následující časové úseky (kvadratury) a zapišme odchylky podle sloupce MO-MS z výše uvedené tabulky:
Time- Departures period sign maxima minima ------------------------------------ 1543-1586 - 1586-1628 + 1628-1671 - 1671-1714 + 1714-1757 - 1718-1761 1745-1765 1757-1800 + 1769-1788 1777-1799 1800-1842 - 1805-1830 1810-1832 1842-1885 + 1838-1871 1844 1885-1928 - 1884-1928 1856-1943 1928-1971 + 1938-2004 1954-2008 1971-2014 - ????????? 2014-2057 +
Pro období 1714 -1971 se zdá vše fungovat vcelku dobře. Toto pravidlo ale (stejně jako pravidlo z odstavce Koincidence geometrických os) selhává- a opět zhruba po roce 1960!?)
Korekce extrémů WO
Nechť dUN = Neptune.Longitude - Uranus.Longitude, dJJa = Jupiter.Longitude - Jupiter.LongPerihelion - 180 a hledáme extrémy kdee dUN + korekce = dJJa (s danou přesností, např. 5 st.).
Následující funkce byla odvozena podle předchozího odstavce: f = Cos(2*dUN) * abs(Cos(2*dUN)) = sign(Cos(2*dUN)) * Cos2(2*dUN) s korekčním úhlem rovným k * f. Pro hodnotu konstanty k = 120 dostaneme následující tabulku:
Tabulka upravených extrémů
Odstup Teorie Jp J S U N f(dUN) Úprava Pozorování
------------------------------------------------------------------------------
11,28 1749,39 - 15 346 231 322 118 +0.38 1750,73 1750.3 *
1757
11,25 1760,65 - 14 326 358 6 143 0.00 1760,72 1761.5 *
11,20 1771,84 + 14 305 146 51 167 -0.30 1770,79 1769.7 *
11,09 1782,93 + 13 281 276 98 191 -0.87 1779,56 1778.4 *
11,01 1793,94 + 14 256 46 148 215 -0.70 1791,19 1788.1 ?
1800
10,92 1804,86 - 15 229 191 200 238 +0.06 1805,13 1805.2 *
10,92 1815,79 - 15 203 314 249 262 +0.98 1819,56 1816.4 ?
11,01 1826,79 - 14 179 92 296 286 +0.73 1829.80 1829.9 *
11,14 1837,94 + 14 159 233 340 310 +0.21 1838,80 1837.2 .
1842
11,17 1849,11 + 14 140 359 24 334 -0.02 1849,04 1848.1 *
11,17 1860,28 + 14 119 147 69 359 -0.48 1858,55 1860,1 *
11,12 1871,39 + 15 97 277 118 24 -0.99 1868,05 1870,6 ?
10,98 1882,37 - 15 69 48 169 48 -0.29 1881,41 1883,9 ?
1885
11,01 1893,38 - 14 41 193 220 72 +0.25 1894,28 1894,1 *
11,14 1904,52 - 14 17 318 270 97 +1.00 1908,13 1907,0 *
11,23 1915,75 - 14 356 101 315 122 +0.66 1918,04 1917,6 *
11,34 1927,08 - 16 338 242 360 147 +0.14 1927,54 1928,4 *
1928
11,23 1938,31 + 16 317 10 44 171 -0.08 1938,11 1937,4 *
11,12 1949,42 + 14 294 157 91 195 -0.63 1947,03 1947,5 *
10,98 1960,40 + 14 267 284 141 218 -0.99 1956,54 1957,9 *
10,90 1971,30 + 14 239 55 192 242 -0.03 1971,21 1968,9 ?
1971
10,95 1982,25 + 15 214 199 242 265 +0.68 1984,90 1979,9 ??
11,03 1993,29 + 16 191 323 289 289 +0.94 1997,03 1989,6 ??
11,12 2004,40 + 15 170 105 334 313 +0.47 2006,28 2000,5 ??
11,14 2015,55 14 150 243 17 338 +0.78 2015,70 ?
2014
Řádky s "přijatelnými" výsledky jsou označeny hvězdičkami.
Jiné rezonance
Výpis
Rezonance sledované výše nejsou jediné, které produkují cykly s periodou blízkou periodě sluneční aktivity. Například (J/1,-S/2,+U/4,-N/3) = 21.8 let zatímco (J/1,-S/3,+U/4,-N/2) = 55.8 let. Také (S/1,+U/3,-N/4) = 22.0 let, tedy např. cos(Ls+3*Lu-4*Ln) osciluje s 11-ti letou periodou apod.
J S U N k*W M
------------------------------------
0 3 1 -4 11,2 -971,5
1 0 2 -3 11,1 -1671,2
2 -3 3 -2 11,1 -5971,4
0 1 3 -4 22,0 7807,8
1 -1 -1 1 22,5 -1376,5
0 1 -1 0 45,4 -1724,2
1 -2 0 1 44,5 -6717,5
0 0 2 -2 85,7 2829,8
0 1 -3 2 96,3 -1072,9
1 -3 3 -1 82,7 1275,0
Rezonance se zahrnutím Saturnu
Povšimněmě si nyní rezonance s periodou 44.5 let podle řádku:
J S U N k*W M ------------------------------------ 1 -2 0 1 44,5 -6717,5
Po přepisu na tvar:
LJ - 2* LS + LN = LJP + k*π/2
dostaneme nové hodnoty WN (porovnáme je s extrémy WO):
Odstup WN WO 0,00 1605,503 1605,6 9,09 1614,593 1613,1 14,84 1629,433 1627,6 8,27 1637,701 1638,5 10,82 1648,516 1649,4 13,03 1661,548 1660,5 8,10 1669,652 1671,6 14,26 1683,917 1682,8 9,67 1693,582 1694,0 9,75 1703,329 1705,0 13,61 1716,936 1716,0 9,42 1726,355 1727,1 11,80 1738,155 1738,2 12,21 1750,366 1749,5 9,34 1759,702 1760,8 13,53 1773,228 1772,0 9,91 1783,139 1783,1
Odstup WN WO
9,75 1792,886 1794,1
14,35 1807,232 1805,0
8,19 1815,419 1815,9
12,70 1828,123 1826,9
11,14 1839,266 1838,1
8,27 1847,534 1849,3
14,59 1862,127 1860,4
9,25 1871,382 1871,5
10,16 1881,539 1882,5
13,28 1894,818 1893,5
9,34 1904,154 1904,7
12,54 1916,694 1915,9
11,47 1928,166 1927,2
9,75 1937,913 1938,4
13,61 1951,520 1949,6
9,58 1961,103 1960,5
Odstup WN WO 10,98 1972,082 1971,4 13,11 1985,196 1982,4 8,27 1993,465 1993,4 14,10 2007,565 2004,6 9,58 2017,148 2015,7 8,52 2025,663 2026,8 14,76 2040,420 2037,9 8,76 2049,181 2049,0
- Dobrá shoda mezi extrémy WN a WO existuje díky rezonanci [J/3, -S/8, -U, N/5] (dá se odvodit z rozdílu výrazů pro WN a WO jako funkce longitud planet...). Vedoucí perioda této rezonance je (J/3, S/8) = 53.555 let (tj. B/8, dělitel Babylónské periody B).
- Ale - jestli mají být všechny periody měřeny vzhledem k Jupiterovu perihelu, nebo k jiným bodům (např. každá planeta ke svému perihelu apod.) - není jasné.
- Hodnoty odstupů (tj. vzdálenosti 2 sousedních extrémů) se zdají být bi-modální, podobně jako u skutečných slunečních cyklů. Neodpovídají ale pozorovaným odstupům.
Další pozorování
Významná odchylka
Období let 1761 - 1805 (s centrem okolo r. 1783) by mohlo být důležité. Extrémy sluneční aktivity očekáváme v letech označených # (liché řádky), ale skutečná aktivita byla pozorována spíše v letech označených hvězdičkami:
Theory Jp J S U N Observation ------------------------------------------------------- # 1760,65 *** 14 326 358 6 143 1761.5 1765,96 14 136 66 27 154 # 1771,85 *** 14 305 146 51 167 1769.7 1777,08 *** 13 115 211 73 179 1778.4 # 1782,94 13 281 276 98 191 1788,14 *** 13 90 334 122 202 1788.1 # 1793,94 14 256 46 148 215 1799,14 14 63 117 173 226 # 1804,87 *** 15 229 191 200 238 1805.2
V r.1783 nastává jistá symetrie nebo kolmost, zarovnání vnějších planet (viz obrázek planetárního postavení - perihel Jupitera je na pravé straně obrázku...!?)