Sluneční aktivita - Úvod

Periodické změny

Pozorování Slunce

Thomas Harriot (1610), Galileo Galilei, Johan Fabricus (1611), Christoph Scheiner (1611-1633),
Johannes Baptista Cysat, Jean Tarde (1615-1619), Charles Malapert (1618-1626), Danie Mogling (1626-1629),
Pierre Gassendi (1631-1646), Johannes Hevelius (1652-1685), Jean Picard (1650-1685), Robert Boyle (1661),
Phillipe La Hire(1700-1718), Francois de Plantade (1704-1726), Christian Horrebow (1761-1776), Alexander Wilson (1774),
William Herschel (1800-1826), Samuel Heinrich Schwabe (1826-1868), Rudolf Wolf (1847-1893), ...
Ma Tuan Siena (Čína, 301-1205), Hiraiama (Tokio,188-1638)

Pohyb Slunce

Podle Newtona neobíhá Země (E) okolo Slunce (C), ale obě tělesa se pohybují okolo svého společného těžiště G(C,E). Totéž platí také pro Zemi a Měsíc (L), Navíc není to Země, ale G(E,L) co se pohybuje okolo G(C,E)...

Při uvažování více planet se vše začíná dále komplikovat: Slunce vykonává složitý pohyb jako odpověď na pohyb planet.

Hlavní postup Slunce je zapříčiněn Jupiterem a Saturnem, které – vzhledem k poměru period 5:2- nutí Slunce k pohybu po dráze připomínající trojlístek. Těžiště G(C,planety) se pohybuje buď uvnitř Slunce (cca 36% času), nebo se od okraje Slunce výrazně nevzdaluje. Jen když Jupiter míjí planetu Saturn, dosahuje vzdálenost těžiště od Slunce až cca 2.2 RS (kde RS je poloměr Slunce).

Slunce se pohybu vynucovanému pohybem planet brání. Zpětným vlivem na planety může tak působit jistou synchronizaci pohybu všech těles.

Vzdálenost Slunce-těžiště
 

a 108 [km]

M/ mi [10³]

Di [km]

Jupiter

7.78

1.0474

742792.0

Saturn

14.3

3.4981

408793.0

Neptun

45.0

19.314

232992.0

Uran

28.7

22.869

125497.0

Vzdálenost Slunce od těžiště soustavy

Na vzdálenosti Slunce od těžiště soustavy se podílí především vnější planety (J,S,N,U), ostatní známá tělesa mají nepatrný vliv.

Jen odchylka působená Jupiterem (742792 km) vysouvá těžiště za okraj Slunce (Rs~696000 km).

Celková vzdálenost těžiště činí D=∑Di, kde Di = ai * mi/M, ai je vzdálenost planety od Slunce, mi hmotnost planety a M celková hmotnost. Hmotnost Slunce MSLUNCE~1990.00 [1027kg], hmotnost všech planet ∑mi ~2.67 [1027kg]. Protože ∑mi je malé vzhledem k MSLUNCE je hmotnost celé soustavy M~MSLUNCE.

Rychlost a zrychlení Slunce

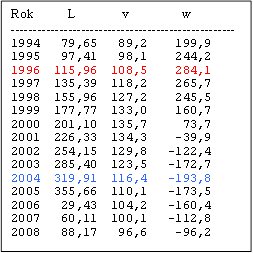Rok L v w --------------------------------------------------- 1994 79,65 89,2 199,9 1995 97,41 98,1 244,2 1996 115,96 108,5 284,1 1997 135,39 118,2 265,7 1998 155,96 127,2 245,5 1999 177,77 133,0 160,7 2000 201,10 135,7 73,7 2001 226,33 134,3 -39,9 2002 254,15 129,8 -122,4 2003 285,40 123,5 -172,7 2004 319,91 116,4 -193,8 2005 355,66 110,1 -173,5 2006 29,43 104,2 -160,4 2007 60,11 100,1 -112,8 2008 88,17 96,6 -96,2 Rychlost (v) i zrychlení (w) se poměrně výrazně mění. Hlavní perioda změn vychází z (J,S) ~19.86 let.

Obdobně jako se (z příčiny eliptických drah planet) mění odstupy konjunkcí J-S:1940.85 ( 20.41) 1961.26 ( 20.01) 1981.28 ( 19.15) 2000 mění se také odstupy největších zrychlení 1938 (18) 1956 (20) 1976 (20) 1996 a největších zpomalení 1947 (20) 1967 (22) 1989 (15) 2004 Slunce (vzhledem k barycentru). 

    Rok     L       v         w
   ----------------------------------
    1938   150,5    115,8     251,3
    1947     7,0    105,1    -212,8
    1956   355,0    105,6     164,7
    1967   292,4    102,7    -224,1
    1976   233,9    105,0     211,0
    1989   160,9     92,7    -276,2
    1996   116,0    108,5     284,1
    2004   319,9    116,4    -193,8

I přes proměnlivost odstupů extrémů (cca 15-22 let) je za vším stále perioda (J,S) ~19.86 let.

Pozorování zrychlení Slunce nevede přímo k příčině primárního 11-ti letého cyklu Sluneční aktivity.

Více o cyklech sluneční aktivity je na stráncee Sluneční cykly.

Dlouhodobé změny

V letech 1810-1812 (Daltonovo minimum) byl Jupiter v opozici proti Saturnu, Uranu a Neptunu (J-SUN).
Obdobná taková konfigurace planet nastala například v letech 1989-1991.

1.1.1811 s_longterm2 1.1.1990 s_longterm4

Další konfigurace (Daltonovské extrémy) najdeme v letech (tučně modře – minima, tučně červeně – maxima):
84-85, 124-126, 263-265, 303-304,442-444, 483, 621-623, 762, 800-801,
1134, 1314, 1492, 1631, 1671, 1810-1812, 1850, 1989-1991, 2029-2030, 2168-2170.

Pokud opozice J-SUN implikuje minimum sluneční aktivity, pak je nutné vysvětlit nárůst aktivity v letech 1134 (středověké maximum) a 1989-1991 (novověké maximum).

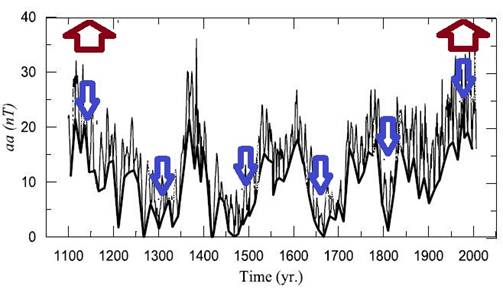s_longterm6 (graf – geomagnetický index - prof.Silvia Duhau).