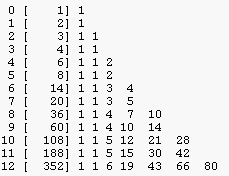Schematická algebra - G-Systémy

G-Systémy - Algebraická teorie hudebních struktur
V tomto textu je představena algebraická teorie souzvukových druhů. Každé uskupení tónů je zobrazeno jako instance takzvaného G-systému. Cílem je opatřit jednoduchý algoritmus pro generování hudebních struktur. Mohl by být užitečný pro programátory zabývající se počítačovou hudbou nebo analýzou hudby. Teorie G-systemů dává některé známé matematické výsledky jednoduchým a jasně uspořádaným způsobem. Proto by mohla být inspirující pro matematiky studující metody enumerací, teorii grup, algebraická řešení kombinatorických problémů a jiné oblasti (Fermatovy věty, Gaussova theorie tříd rovnic, Polyova enumerace, Sylowovy grupy,..).
- 1.G-systémy a jejich instance
- 2.Enumerace druhů
- 3.Skladba G-systémů
- 4.Binární G-systémy
- Závěr
- Literatura
1.G-systémy a jejich instance
Oblast, kterou zde studujeme, je v kombinační teorii známa jako Kombinatorika náhrdelníků (Combinatorics of necklaces).
1.1 Základní definice
Uvažujme uspořádání n prvků do k buněk. Nechť A je množina s n členy (prvky) a množina E(A) = {0, 1, .., n-1} báze množiny A. Nechť B je množina s k členy (buňkami) a ξ relace z E(B) do E(A).
ξ
(buňky) E(B) ------------- E(A) (prvky)
Nechť čísla E(B) jsou pozice čísel (číslic) z E(A). Přepisem do n-kové
soustavy získáme nk možných čísel. Označme množinu všech těchto čísel be
M()=M(n,k). Členy této množiny jsou tzv. instance.
Např. množiny A={p, q}, B={x, y, z} mají báze E(A)={0, 1}, E(B)={0, 1,
2}. Systém M(2,3) má 23=8 instancí {000, 001,.., 111}.
Množinu M()=M(n,k) (s relací ξ) budeme nazývat systém stupně n a řádu k.
Jestliže ξ je relace ekvivalence, je možné rozlišit druhy instancí. Druhy
jsou výsledkem rozkladu M()/ξ. Každý druh má své reprezentanty. Počet
transpozic znamená počet členů druhu.
V případě 12-ti tónového temperovaného hudebního systému máme n=2, k=12.
Např. nechť A={existuje, neexistuje} a B={c, c#, d, d#, e, f, f#, g, g#,
a, a#, h}. Báze E(A)={0,1}, E(B)={0, 1, .., 11} a relace ξ utvářejí
system M(2,12). Instance 001001001001 representuje tónové uskupení [c,
d#, f#, a] a má dvě transpozice 010010010010, tj. [c#, e, g, a#] a
100100100100 tj. [d, f, g#, h]. Zmenšený septimový akord je druh z
M(2,12) s 3-mi transpozicemi.
1.2 G-relace
Budiž relace G, definována následovně, nazývána G-relace.
u(i,j) = nj * g(i) ( mod(r-1))
Číslo r je (v tomto článku) vždy předpokládáno rovné celkovému počtu instancí, tj. r = nk. Číslo g(i) is číslo reprezentanta, u(i,j) jsou čísla instancí.
Systemy s G-relací nazýváme G-systemy, G()=G(n,k). Každý G(n,k) má m(n,k) druhů označených g(i), i=1..m.
1.3 Čísla instancí
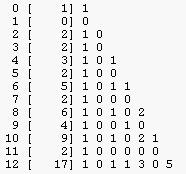
Zapišme přehled všech instancí uspořádaný podle druhů. Přehled pro G(n,k) má k sloupců (k je nejvyšší možný počet transpozic). 16 instancí z G(2,4) vytváří 6 druhů.
Instance G(2,4)
| 1 |
0 0 0000 0
0 0
|
| 2 |
0 0 0 1 1 0 0 0 0001 0010 0100 1000 1 2 4 8
0 1 0 0 0 0 1 0
|
| 3 |
0 1 1 1 1 0 0 0 0011 0110 1100 1001 3 6 12 9
0 1 0 0 1 0 1 1
|
| 4 |
1 0 0 1 0101 1010 5 10
0 1 1 0
|
| 5 |
1 1 1 1 1 0 0 1 0111 1110 1101 1011 7 14 13 11
0 1 1 0 1 1 1 1
|
| 6 |
1 1 1111 15
1 1
|
1.4 Generování čísel instancí
Algoritmus je podobný Eratosthenovu sítu pro vyčlenění prvočísel z přirozených čísel. V našem případě vyčleňujeme čísla representantů druhů z čísel všech instancí. Transpozice instancí jsou analogie prvočíselných násobků v Eratosthenově sítu.
vyprázdni množinu M
↓
+--+- pro g=0 až (nk-1-1) -- zapiš poslední druh
| | | g=nk-1
| ↑ je druh g v M ?
| | |
| +- ANO-----+
| |NE
| |
| zapiš g do M
| ↓
| instance u <- g
| |
|+---> dokud není u v M ----+
|| | |
|| zapiš u do M |
|| | |
|| transpozice instance |
|| u <- n * u |
|+------<-----+ |
+-------------<-------------+
Příklady výstupu:
G(n,1)
G(2,1) G(3,1) G(4,1)
0 0 0
1 1 1
2 2
3
G(2,2) G(3,2) G(4,2)
0 0 0 6 9
1 2 1 3 1 4 7 13
3 2 6 2 8 10
4 3 12 11 14
5 7 5 15
8
G(2,3) G(3,3) G(4,3)
0 0 0 21
1 2 4 1 3 9 1 4 16 22 25 37
3 6 5 2 6 18 2 8 32 23 29 53
7 4 12 10 3 12 48 26 41 38
5 15 19 5 20 17 27 45 54
7 21 11 6 24 33 30 57 39
8 24 20 7 28 49 31 61 55
13 9 36 18 42
14 16 22 10 40 34 43 46 58
17 25 23 11 44 50 47 62 59
26 13 52 19 63
14 56 35
15 60 51
1.5 Dělitelnost v G(n,k)
Číslo instance u(i,j) je relativním prvočíslem s r -1 = nk -1 jen když
odpovídající číslo druhu g(i) je relativním prvočíslem s r -1. Počet
všech instancí, která jsou relativními prvočísly s r -1 je φ(r), kde φ je
Eulerova funkce. Jestliže g(i) relativním prvočíslem s r -1, pak jeho
druh musí být vlastní (ne vnořený) a takový druh má k instancí.
Proto: φ(nk -1)= 0 (mod k)
V G(2,4) jen tyto instance jsou relativní prvočísla s 24 -1=15: (1, 2,
4, 8) a (7, 14, 13, 11). A φ(24 -1) = φ(15) = 8; 8 = 0 (mod 4).
2.Enumerace druhů
Jedno z prvních řešení problému, který studujeme, bylo publikováno Gaussem v jeho algebraické theorii tříd rovnic [Gauss,1959]. Polya předvedl obecné kombinatorické řešení pro počítání struktur. Jeho enumerační věta [Preparata,1974] byla navržena pro počítání tříd s ohledem na libovolné operace symmetrie. Akordické hudební struktury mají jen jednu takovou operaci - rotaci. Tento fakt nám umožňuje použít jednoduchý algoritmus.
2.1 Vnořování
Pro každé d|k existuje system G(n,d) vnořený do G(n,k). Vnořený druh g' v
G(n,k) je podobný svému výchozímu druhu g z G(n,d). Skutečně původní
druhy jsou nazývány vlastní druhy. Podobnost s výchozími druhy znamená
týž počet transpozic a podobné instanční struktury. System G(n,p), p je
prvočíslo, má právě jeden vnořený system G(n,1). Pro g z G(n,d), g' z
G(n,k), d|k platí: g' = c . g kde c ke keficient vnoření definovaný
následovně:
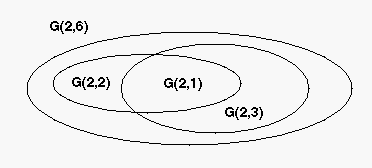
c(d,k) = (nk-1) / (nd-1). Např. systém G(2,6) získává (dědí) vnořené
systémy G(2,1), G(2,2) a G(2,3);
G(2,1) je také vnořený do G(2,2) a G(2,3).
Jiný příklad: systém G(2,4) dědí vnořené systémy G(2,1) a G(2,2); viz např. druh g(2) = 1 v G(2,2) a jí odpovídající druh g(4) = 5 v G(2,4) s koeficientem vnoření c(2,4) = 5.
G(2,1): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1
G(2,2): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1 u(1,2)= 2 g(3)= u(0,3)= 3
G(2,4): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1 u(1,2)= 2 u(2,2)= 4 u(3,2)= 8 g(3)= u(0,3)= 3 u(1,3)= 6 u(2,3)=12 u(3,3)= 9 g(4)= u(0,4)= 5 u(1,4)=10 g(5)= u(0,5)= 7 u(1,5)=14 u(2,5)=13 u(3,5)=11 g(6)= u(0,6)=15
G(2,1) - G(2,2): c(1,2) = (22 -1) / (21 -1) = 3 G(2,2) - G(2,4): c(2,4) = (24 -1) / (22 -1) = 5
2.2 Rekurentní vztahy
Nechť v(n,k), w(n,k) a m(n,k) jsou počty vlastních, vnořených a všech
druhů v G(n,k). Platí:

Specielně pro prvočíslo p je:

Např. System G(2,6) má 14 druhů (9 vlastních + 5 vnořených):
Počítání druhů v G(2,6)
|
Vlastní druhy |
Vnořené druhy |
|
v(2,1)=2/1=2 |
w(2,1) = 0 |
|
v(2,2)=(22-1v(2,1))/2= 1 |
w(2,2) = v(2,1) = 2 |
|
v(2,3)=(23-1v(2,1))/3= 2 |
w(2,3) = v(2,1) = 2 |
|
v(2,6)=(26-1v(2,1)-2*v(2,2)-3*v(2,3))/6 = 9 |
w(2,6) = v(2,1)+v(2,2)+v(2,3)= 5 |
Proto m(2,6)= v(6) +w(6) = 9 +5 = 14 druhů.
Gauss [CG1} předložil předchozí rekurentní rovnice v elegantním, kompaktním tvaru: nk = ∑d(d) tj. v naší terminologii: nk = ∑{d|k} d*v(n,d).
2.3 Zjednodušování
Vyčísleme součty všech druhů m(n,k) pro jednotlivé řády k jako funkce n:
k=1: m(n,1)= 1/1 (n) + 0 = n k=2: m(n,2)= 1/2 (n2- n)+ n = 1/2 (n2+n) k=3: m(n,3)= 1/3 (n3-n)+ n = 1/3 (n3+ 2n) k=4: m(n,4)= 1/4 (n4-n2)+ 1/2 (n2+n) = 1/4 (n4+ n2+2n) k=5: m(n,5)= 1/5 (n5-n) + n = 1/5 (n5+ 4n) k=6: m(n,6)= 1/6 (n6-n3-n2+n)+1/6(2n3+3n2+n)= 1/6 (n6+n3+2n2+2n) k=7: m(n,7)= 1/7 (n7-n) + n = 1/7 (n7+ 6n) k=8: m(n,8)= 1/8 (n8-n4)+ 1/4(n4+n2+2n)=1/8(n8+n4+2n2+4n)
V případě rotačních operací dává Polyova teorie tento výsledek [Beckenbach,1964]:
m(n,k) = 1/k ∑{d|k} φ(d)* nk/d (including d=k),
kde φ je Eulerova funkce.
3.Skladba G-systémů
3.1 Segmentace
Vnořování (ukázané v předchozích odstavcích) je záležitostí G-systemů s
konstantním n.
Nyní budeme vyšetřovat G-systemy s konstantním k. Tyto systémy také mají
něco společného.
Např. podívejme se na systémy G(2,2) a G(3,2). Druhý je jen rozšířením
prvního.
G(3,2) jako rozšíření G(2,2)
G(2,2) = G(3,2)
0 0
1 2 1 3
3 4
6 2
7 5
8
|
Každý G(n,k) má n druhů vnořených z G(n,1). Předpokládejme, tyto druhy
rozdělují G-system do segmentů. Nechť s (s<n )="" takov="" segment=""
representantem="" tohoto="" segmentu="" s="" je="" číslo="">
g(s) = (n-s) * (nk-1) / (n-1).
Jestliže nějaký segment existuje v G(n,k), pak podobný segment existuje
také v G(n+1,k). Tato myšlenka se objasní, když přepíšeme všechna čísla u
čísly (nk-1)-u.
Segmentace G(3,3)
u
0 segment 2
1 3 9
2 6 18
4 12 10
5 15 19
7 21 11
8 24 20
------------------
13 segment 1
14 16 22
17 25 23
------------------
26 segment 0
|
(nk-1)-u = 27-u
0 segment 0
------------------
9 1 3
12 10 4
13 segment 1
------------------
18 2 6
19 5 15
21 11 7
22 14 16
24 20 8
25 23 17
26 segment 2
|
3.2 Číselné soustavy
Zapišme čísla nk-1-u z předchozí tabulky jako funkce n a podívejme se na koeficienty polynomů:
k=2 k=3
segment 0 segment 0
1 1
segment 1 segment 1
n 1 n2 1 n
n+1 n2+n n2+1 n +1
n2+n+1
k=2 k=3
segment 0 segment 0
0 0 0 0 0
segment 1 segment 1
1 0 0 1 1 0 0 0 0 1 0 1 0
1 1 1 1 0 1 0 1 0 1 1
1 1 1
Každý G-system je množinou čísel z n-kové číselné soustavy. G-relace rozděluje G(n,k) do n segmentů, kde každý segment s užívá právě s symbolů, s=0..n-1.
Skladba G-systemů
G(1,2) 00 00 00
----------------------------
10 01 10 01 10 01
G(2,2) 11 11 11
----------------------------
20 02 20 02 20 02
21 12 21 12 21 12
G(3,2) 22 22 22
----------------------------
30 03 30 03
31 13 31 13
32 23 32 23
G(4,2) 33 33
----------------------------
40 04
41 14
42 24
43 34
G(5,2) 44
----------------------------
|
G(1,3) 000 000 000
--------------------------------------------
100 001 010 100 001 010 100 001 010
110 101 011 110 101 011 110 101 011
G(2,3) 111 111 111
--------------------------------------------
200 002 020 200 002 020
201 012 120 201 012 120
210 102 021 210 102 021
211 112 121 211 112 121
220 202 022 220 202 022
221 212 122 221 212 122
G(3,3) 222 222
--------------------------------------------
300 003 030
301 013 031
302 023 032
310 103 130
311 113 131
312 123 132
320 203 230
321 213 231
322 223 232
330 303 330
331 313 331
332 323 332
G(4,3) 333
--------------------------------------------
-------------------------------------------- |
Součet polynomických koeficientů je stejný pro všechny instance daného druhu (instance téhož druhu mají stejnou úroveň).
4.Binární G-systémy
Binarní systém G(2,k) is zvláštní případ G-systemu, n=2. Je vhodný pro klassifikaci hudebních struktur.
4.1 Distanční schema
V binarním systému (base E(A) ={0, 1}) je snadné vyjádřit strukturu
instancí.
Nechť úroveň druhu L je počet číslic "1" v instanci a nechť interval je
vzdálenost mezi dvěma číslicemi "1". Distanční schéma je výpis všech
sousedících intervalů, poslední interval v závorkách, [Janecek,1959].
Distanční schéma instancí v G(2,4))
i g(i) Instance čísla (binary) Schema Level ------------------------------------------------------ 1 0 0000 (0) 0 2 1 0001 0010 0100 1000 (4) 1 3 3 0011 0110 1100 1001 1(3) 2 4 5 0101 1010 2(2) 2 5 7 0111 1110 1101 1011 1 1(2) 3 6 15 1111 1 1 1 (1) 4 |
4.2 Trojúhelníky
Poslední sloupec předchozí tabulky zobrazuje úroveň odpovídajícího druhu, tj. úroveň instancí druhu. Spočítejme kolik instancí a druhů je na každé úrovni.
Počítání v G(2,4)
Úroveň 0 1 2 3 4 -------------------------------------------- Všechny instance 1 4 6 4 1 Vnořené instance 1 0 2 0 1 Vlastní instance 0 4 4 4 0 -------------------------------------------- Všechny druhy 1 1 2 1 1 Vnořené druhy 1 0 1 0 1 Vlastní druhy 0 1 1 1 0 |
Následující schemata zobrazují totéž (strukturováno do trojúhelníků) pro
všechna G(2,k). První sloupec zobrazuje řád k daného G-systemu, v dalších
sloupcích jsou počty pro jednotlivé úrovně. Poslední sloupce obsahují
součty instancí a druhů. Trojúhelníky jsou symmetrické, zapisujeme jen
jejich polovinu.
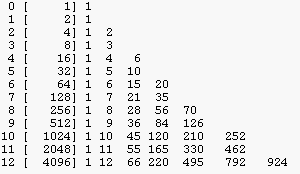
Např. v 12-ti tónové hudbě je 220 trojzvuků, 19-ti druhů. Těchto 19 druhů
znamená, že existuje 19 typů trojzvuků (moll, dur, zvětšený, zmenšený,
...). Jeden jediný druh (zvětšený trojzvuk) je vnořený. Tento druh má 4
instance. Proto je 220-4=216 vlastních instancí trojzvuků a 216/12 = 19-1
= 18 vlastních druhů trojzvuků.
k (0)(1)(2)(3) (4) (5) (6) (7) (8) (9)(10)(11)(12) ---------------------------------------------------------------------- 12 1 12 66 220 495 792 924 792 495 220 66 12 1 všechny instance ---------------------------------------------------------------------- 1 1 1 2 0 2 0 3 0 3 3 0 vnořené instance 4 0 4 4 4 0 6 0 6 12 18 12 6 0 ---------------------------------------------------------------------- 12 0 12 60 216 480 792 900 792 480 216 60 12 0 vlastní instance 12 0 1 5 18 40 66 75 66 40 18 5 1 0 vlastní druhy ---------------------------------------------------------------------- 1 1 1 2 0 1 0 3 0 1 1 0 vnořené druhy 4 0 1 1 1 0 6 0 1 2 3 2 1 0 ---------------------------------------------------------------------- 12 1 1 6 19 43 66 80 66 43 19 6 1 1 všechny druhy
Trojúhelník vlastních instancí a vlastních druhů
|
|
|
Trojúhelník vnořených instancí a vnořených druhů
|
|
|
Trojúhelník všech instancí (Pascalův) a všech druhů
|
|
|
Celkový počet vnořených instancí stejně tak jako vnořených druhů v
systému s prvočíselným k je roven 2. Počet vlastních instancí je vždy
k-násobkem počtu vlastních druhů.
více
Závěr
V článku byl představen náhled do problému hudebních structur. Výsledky
byly porovnány s podobnými výsledky získanými Gaussem a Polyou. Teorie
G-systémů má také vazby do jiných matematických oblastí.
Např. omezení systemů
(r<nk) vede k teorii primitivních kořenů;
rozložení prvočísel
v jednotlivých druzích by mohlo poskytnout nějaké informace
o prvočíslech;...
Zvláště
trojúhelník vlastních druhů
by mohl být zajímavý. S jeho strukturou jsou spojeny
některé věty o prvočíslech (Wilsonova věta,...). Trojúhelník se zdá být
obecnější než Pascalův trojúhelník - Pascalův může být získán integrací
jeho členů.
Teorie byla prezentována v poster-sekci Conference on Computational and
Mathematical Methods in Music, ve Vídni, 1.-4.prosince 1999 (Diderot
Forum on Mathematics and Music). Text, jenž následuje, pokrývá a
rozšiřuje text otištěný ve sborníku konference.
Na začátku jsem nazýval tyto systémy pojmem "Genetické systémy", pro
jistou analogii s dědičností (viz Vnořování G-systemů). Později jsem
jméno zkrátil na "G-systemy". Na teorii jsem pracoval převážně v letech
1990-1992. V letech následujících, 1993-1996, pak hledal podobné teorie v
literatuře.
Enumerace celkového počtu druhů v G-systemu je shodná s enumerací
celkového počtu tříd rovnic, která byla studována Carl Fridrichem Gaussem
zhruba před 200 lety. Takže písmeno G ve jménu "G-system" by mohlo být
spojeno s Gauss. Byl pravděpodobně první, kdo znal a popsal tyto
matematické konstrukce.
Literatura
Gauss,1959 Gauss Carl Fridrich: Trudy po teorii cisel (Ucenie o vycetach
II),p.782) (Works on Theory of Numbers; in Russian), Moscow 1959.
Janecek,1959 Janeček Karel: Základy moderní harmonie (Fundamentals of
Modern Harmony; in Czech), Prague 1965.
Beckenbach,1964 Edwin F.Beckenbach, George Polya: Applied Combinatorial
Mathematics University of California, John Wiley and Sons,Inc , New York,
1964.
Preparata,1974 Franco P.Preparata, Raymond T.Yeh Introduction of Discrete
Structures Addison-Wesley Publishing Company Inc., U.S.A., 1974.