Schematická algebra - Aplikace

Hudební struktury

Tónová uskupení

Tónová uskupení mají některé specifické vlastnosti. Souzvuky - například durový trojzvuk {c,e,g} - je možné postavit obvykle na každý tón. V 12-ti tónové soustavě je 12 různých durových trojzvuků (12 transpozic daného trojzvuku). Ale trojzvuk {c,e,g#} neexistuje v tolika variantách. Již pátá transpozice {e,g#,c} je (bez ohledu na pořadí tónů) totožná s původním souzvukem. Trojzvuk {c,e,g#} má tedy jen 4 transpozice.

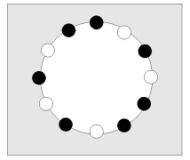
g_gbsyst

Všech existujích různých souzvuků (včetně ticha a 12-ti zvuku) je 2¹², tj. 4096. Kdyby každý souzvuk bylo možné 12x transponovat (což už např. u ticha ani 12-ti zvuku není možné) muselo by být číslo dělitelné beze zbytku 12-ti (což není, hodnota 4096/12 činí cca 341.33). Ve skutečnosti existuje v 12-ti tónové soustavě 352 druhů souzvuků.

V polovině minulého století vypsal Karel Janeček v knize Moderní harmonie [Janeček] detailně všechny varianty souzvuků (včetně jejich charakteristik...).

Každý souzvuk můžeme nahradit binárním číslem. Když pak binární čísla přepíšeme z dvojkové soustavy do desítkové budeme moci postupně na struktury zapomenou a příčinu různorodosti souzvuků hledat v samotných vlastnostech přirozených čísel.

Čísla instancí

K pochopení, proč souzvuky s méně transpozicemi vznikají, je vhodné postupně kreslit všechny L-zvuky existující v soustavách s k tóny pro k=1,2,3,4,5,.... Matematické struktury odpovídající souzvukům nazveme instancemi. Zápisem jednotlivých transpozic do řádek dostaneme

charakteristická schemata, obecně budeme mluvit o G-systémech stupně n a řádu k, G(n,k).

G-systém G(2,4)

V případě k=4 se množina všech 2⁴=16-ti instancí rozpadne do 6-ti druhů, odpovídající G-systém G(2,4) má následující strukturu:

Distanční schemata

Vzdálenosti mezi tóny, tj. mezi jedničkami ve schematech, se v hudbě nazývají intervaly. Distanční schéma je výpis všech sousedících intervalů.

Distanční schéma v G(2,4)

Příklad znázornění a zápisu instancí v G(2,4):

Poslední interval budeme uvádět v závorkách, jak je zvykem v hudební teorii, viz Janečkova orientační schemata v [Janeček].

Úrovní L(instance,druhu) je počet tónů, tj. jedniček (v instanci, druhu).

Modality a módy

Totéž co platí pro souzvukové druhy platí i pro tzv. modality, tj. struktury v nichž se odehrávají určité úseky skladeb (např. jedna krátká píseň často pokrývá právě jednu modalitu).

Příklad - přirozená modalita

V G-systému G(2,12) odpovídá modalita s číslem instance 1387, binárním schematem 010101101011 a distančním schematem 1 2 2 1 2 2( 2) rozložení bílých kláves na klavíru.

Tato modalita má k=12 transpozic, což umožňuje 12 různých hudebních provedení (stupnice či tónina C dur,C# dur, D dur,...až H dur).

Každá modalita (v jakémkoli z 12-ti provedení) má navíc několik módů, tj. několik způsobů v jakém pořadí tóny hrát. Počet způsobů je roven počtu tónů v modalitě, tj. úrovni druhu, v našem příkladě L=7. Módy se v principu neliší od stupnic (stupnice zachovávají názvy módů,...) Dřívější pojmenování stupnic pomalu zaniká. Ze 7-mi módů používaných ve středověku se dnes vyučuje zpravidla jen stupnice dur (iónská) a moll (aiolská).

1387 7 12 010101101011 1 2 2 1 2 2( 2)

Matematické struktury

Polynomy zbytkových tříd

Polynomy třetího stupně nad oborem zbytkových tříd podle modulu 2 tvoří systém G(2,3).

Derivace sníží stupeň polynomů a tím i počet možných polynomů. Derivace polynomů z G(2,3) přejdou (bez ohledu na koeficienty) v instance G(2,2):

Podle modulu 2 se zůstanou jen 2 výsledky x² a x²+1:

a tyto jsou z G(2,1):

Rozšíření konečného oboru

Rozšířením oboru T o prvek q stupně h dostaneme obor, jehož všechny prvky je možné zapsat ve tvaru

a₀ + a₁q + a₂q² +...+ a_h−1q^h−1

Např.

· prvek q určený rovnicí q²=5 rozšíří obor Z o všechna čísla tvaru a₀ + a₁q = a₀ + a₁√5;

· prvek s³=5 o čísla tvaru a₀ + a₁s + a₂s² = a₀ + a₁√5 + a₂(√5)².

Je-li obor koeficientů a0,a1,a2,.. konečný, můžeme vznikající rozšíření znázornit pomocí G-systémů.

Mějme např. obor Z3 s prvky {0,1,2} rozšířený o prvek q, q²=c [Blažek, Koman].

Ze systému G(3,1) získáme systém G(3,2):

Obdobně obor Z2 s prvky {0,1} rozšířený o prvek s, s³=c, dává schema G(2,3):

G-systémy

& grupy

Na G-systémy jsme dosud nahlíželi jen z pohledu teorie čísel. Nyní se pokusíme využít teorie grup.

Grupy a G-systémy mají některé vlastnosti společné:

vnořování nižších systému do vyšších připomíná podgrupy dané grupy,
v G-systémech najdeme analogii Lagrangeovy věty pro grupy.

Grupa instancí druhu

Instance (určené jednoznačně čísly u) jsou rotací základní instance druhu g. Skládání rotací je asociativní (AB)C=A(BC) i komutativní AB=BA. Rotace prvků G-systému řádu k tvoří komutativní grupu řádu k. (Např. každý druh systému G(2,4) představuje rotace čtverce s označenými vrcholy).

Grupa instancí G-systému

Čísla {1,n,n²,n³..,}, kde n je základ G-systému, vytváří cyklickou grupu s generátorem n. V prvním řádku G-systému jsou čísla {1,n,n²,..,n^k−1} mod r, další vlastní řádky G-systému (tj. řádky obsahující vlastní druhy) jsou g-násobky řádku prvního (podle modulu r), kde g je číslo druhu.

Lagrangeova věta

Kdyby byl systém G(n,k) grupou a vnořený systém G(n,d) d|k jeho podgrupou, pak řádem grupy G(n,k) by mohl být modul r odpovídajícího G-systému. Index podgrupy by odpovídal koeficientu vnoření.

V systému G(2,4) by byly dvě podgrupy: G(2,2) a G(2,1), přičemž G(2,1)<G(2,2)<G(2,4). Moduly systémů jsou r(4)=15, r(2)=3 a r(1)=1.

Tomu odpovídá Lagrangeova věta r(1)|r(2)|r(4), tj. 1|3|15.

Do G(2,2) patří instance {0,5,10,15}, tj. po zkrácení koeficientem vnoření {0,1,2,3}. Obdobně G(2,1) má instance {0,15}, po zkrácení {0,1}.

Vnořování a podgrupy

Mezi vnořenými systémy a podgrupami je rozdíl. U G-systémů rozumíme řádem číslo k, zatímco u grup číslo r=n^k−1.

Všechny druhy systémů prvočíselného řádu jsou vlastní. Není ale pravda, že by tyto vlastní druhy byly vždy nesoudělné s modulem r=n^k−1. Tak tomu je jedině, když modul r je prvočíselný, tj. když r je Mersennovo prvočíslo. V opačném případě je druhů nesoudělných s r méně než vlastních.

V případě G(2,11) je k prvočíslo. Číslo r=2¹¹−1 = 2047 = 23∙89 ale prvočíslem není. V G(2,11) existuje φ(2047) = 22∙88= 1936 instancí, tj. 1936/11=176 druhů nesoudělných s 2047. Přitom vlastních druhů v G(2,11) je 2046/11 = 186.

U G-systémů i grup pokračuje vnořování až k strukturám (systémům resp.podgrupám) prvočíselného řádu.

G-systémy s prvočíselným řádem a složeným modulem r mohou mít i jiné než triviální podgrupy!?!

Kompozičnířady

Systémy vnořené do G(n,k), s řády d1|d2|...|k připomínají tzv. kompoziční řady. Např. pro k=12 dostáváme následující 3 řady:

 12, 4, 2, 1
 12, 6, 2, 1
 12, 6, 3, 1

Tyto řady odpovídají třem různým cestám mezi čísly 1 a 12 v diagramu:

      12
    4    6
  2    2    3
       1

Rozdělení druhů

G-relace rozděluje instance do druhů. Určité operace (sčítání i násobení podle modulu r) je možné vykonávat nad celými druhy. Předpokládáme, že vybraný druh můžeme zastoupit libovolnou z jeho instancí. Druhy podle operací rozlišíme do následujících typů:

Vztahy druhů

Nulový druh (0): 0 + g = g (libovolný druh g)
Jednotkový druh (1): 1 ∙ g = g (libovolný druh g)

Kontrastní druh (−g): g + (−g) = 0 (0 nulový druh)

Např.:

  G(2,4): −0=15;  −1=+7;   −3=+3;  −5=+5;
  G(2,5): −0=31;  −1=+15;  −3=+7;  −5=+11;
  G(2,6): −0=63;  −1=+31;  −3=+15; −5=+23; −7=+7;
                  −9=+27; −11=+13; −21=+21;

Inverzní druh g': g ∙ g' = 1 (1 jednotkový druh)

  G(2,4): 1'=1; 7'=7;
  G(2,5): 1'=1; 3'=11; 5'=7; 15'=15;
  G(2,6): 1'=1; 5'=13; 11'=23; 31'=31;

Sdružené druhy g,h: g²=h, h²=g
```
  G(2,4):  −
  G(2,5): 7²=5; 5²=7
  G(2,6): 11²=23; 23²=11
```
Sdružené druhy jsou nutně inverzní (nikoli naopak). Tvoří dvojprvkové cyklické podgrupy.

Dvojice druhů

Rozpad na dvojice druhů.

V případě, kdy se celý G-systém rozpadá na dvojice druhů, platí

2k|(r−1)

   0
   1  2  4  8 16
   3  6 12 24 17
   5 10 20  9 18
 ──────────────────
   7 14 28 25 19
  11 22 13 26 21
  15 30 29 27 23
  31

V systému G(2,5) je celkem 8 kontrastních druhů. Druhy tvoří 4 dvojice (−0=31; −1=+15; −3=+7; −5=+11) Proto 2k|(r−1) tj. 10|(31−1).

Faktorové grupy

Nechť G je multiplikativní grupa a R relace kongruence na této grupě. Pak struktura G/R vytvořená rozkladem G podle kongruence R je také grupa.

Tato grupa se nazývá faktorovou grupou grupy G podle kongruence R.

Inverzní druhy

Zajímá nás zda v mezidruhových operacích (sčítání, násobení) bude existovat ke každému druhu jednoznačně určený druh inverzní.

Inverzní druhy ke všem druhům systému, existují jen v systémech s prvočíselným modulem (rεP), kde jsou všechny druhy (kromě 0) s modulem r nesoudělné.

V G(2,5) jsou všechna g-čísla (kromě 0) nesoudělná s r=31 a tvoří grupu řádu 6:

Problém s inverzními prvky nastává tehdy, když číslo druhu je soudělné s modulem r=n^k−1.
V G(2,4) k prvkům 3 a 5 neexistují inverzní prvky, 3∙5 (mod 15) = 0. Přitom (3,15) ≠ 0 a (5,15) ≠ 0.

Multiplikativní grupu tvoří jen druhy 1 a 7.

Obecně existují inverzní druhy jen pro druhy s čísly nesoudělnými s modulem, tj. pro taková g, že (g,r)=1. V G(2,6) tvoří grupu druhy nesoudělné s r=2⁶−1 = 63:

Inverzní druhy - příklady

D(7,*)
   1 7
 ──────
 1 1 7
 7 7 1

D(15,*)
    1 3 5 7
  ───────────
  1 1 3 5 7
  3 3 3 0 3
  5 5 0 5 5
  7 7 3 5 1

D(31,*)
    1 3 5 7 11 15
 ────────────────────
  1 1 3 5 7 11 15
  3 3 5 15 11 1 7
  5 5 15 7 1 3 11
  7 7 11 1 5 15 3
 11 11 1 3 15 7 5
 15 15 7 11 3 5 1

 D(63,*)
    1 5 11 13 23 31
  ────────────────────
  1 1 5 11 13 23 31
  5 5 11 31 1 13 23
 11 11 31 23 5 1 13
 13 13 1 5 23 31 11
 23 23 13 1 31 11 5
 31 31 23 13 11 5 1

Grupy vyšších řádů

Jedině čísla 1 a 5 v T(6,∙) jsou invertovatelná, tj. k danému x existuje i 1/x (viz) Grupu všech invertovatelných prvků v Zn označíme In.

Když pε P je Ip cyklická grupa.

In je cyklickou groupou, jedině když n=2,4,p^t nebo 2∙p^t (pro pεP, p>2, t≥1).

Cyclic group

Pro n=9=3² dostaneme po vyškrtání vnořených řádek a sloupců cyklickou grupu:

    Grupa            R-systémy  
    1 2 4 5 7 8      R(2,6,9)         R(5,6,9)
    2 4 8 1 5 7       0                0
    4 8 7 2 1 5       1,2,4,8,7,5      1,5,7,8,4,2
    5 1 2 7 8 4       9                9  
    7 5 1 8 4 2    
    8 7 5 4 2 1

Non-cyclic group

Pro n=8=2³ ale vznikající grupa cyklická není (rozpadá se na cyklické podgrupy 2. řádu):

    Grupa        R-system  
    1 3 5 7      R(5,2,8)    R(7,2,8)   
    3 1 7 5       0           0
    5 7 1 3       1,5         1,7
    7 5 3 1       3,7         3,5
                  8           8

Fyzikální struktury

Interakce nukleonů

Schemata binárního systému G(2,k) se ukazují být vhodná take k popisu interakcí nukleonů v jádrech atomů. Uvažujme množinu dvojic prvků dvou druhů p,n, tj. analogii atomového jádra hélia (2 protony + 2 neutrony).

Mezi prvky existují čtyři možné vazby:

    1.p1 - n1
    2.p1 - n2
    4.p2 - n1
    8.p2 - n2

Všechny kombinace existence a neexistence vazeb tvoří instance G(2,4).

Analogické schéma dostaneme také při uvažování druhových jednosměrných vazeb:

    1.p ->p     
    2.p ->n     
    4.n ->p     
    8.n ->n

(Obdobná schémata interakcí použil D.Bruncko v Čs.čas.fyz 41, 1991, při studiu pružných a nepružných interakcí nukleonů).

Rozdělovací funkce

Maxwell, James Clerk

Maxwell, James Clerk [], 1831-1879, (anglický) fyzik, autor obecné teorie elektromagnetizmu. Zabýval se také molekulární fyzikou.

Uvažujme soubor k-částic, z nichž každá může být v některém z n možných stavů. Za předpokladu, že každé uspořádání nastává se stejnou pravděpodobností, dostaneme n^k skupin určených variacemi s opakováním.

Pro k=2, n=3 celkem n^k=3²=9 skupin:

00, 01, 10, 02, 20, 11, 12, 21, 22 Maxwell-Boltzmannovo rozdělení.

V mikrosvětě se ukázal předpoklad rozdělení se stejnou pravděpodobností nesprávný. Částice jsou nerozlišitelné, vytváří skupin určených kombinacemi s opakováním.

Pro k=2, n=3: = = 6 skupin:

Bose-Einsteinovo rozdělení

Za podmínky, že dvě částice nemohou být ve stejném stavu (tzv. Pauliho vylučovací princip) se počet skupin v souboru (podle kombinací bez opakování) zúží na tři, tj. = =3:

Fermiho-Diracovo rozdělení

    01 nebo 10
    02 nebo 20  
    12 nebo 21

V souboru částic, který tvoří instance G-systému očekáváme, že stavy budou vzájemně nerozlišitelné tehdy, pokud budou stejného druhu.

Takové kritérium se ve fyzice nepoužívá, není respektováno ani jednou z uvedených statistik. Struktuře G(3,2) je nejblíže Bose-Einsteinova statistika, obecně je ale založena jinak.

Binární schemata          Instance
─────────────────────────────────────
1/ 0000                   0
2/ 0001 0010 0100 1000    1  2  4  8
3/ 0011 0110 1100 1001    3  6 12  9
4/ 0101 1010              5 10
5/ 0111 1110 1101 1011    7 14 13 11
6/ 1111                  15

V G(2,4) je celkem 16 instancí.

Podle Maxwell-Boltzmannovy statistiky jsou všechny instance stejně pravděpodobné.

Bose-Einsteinova statistika vyčlení 5 skupin, např. 0011 bude ve stejné skupině jako 0101.

Znaménkové systémy

Znaménkový systém S(k) = S(±,k) je podobný binárnímu systému G(2,k). Hledáme možná uspořádání orientovaných šipek (např. spinů elektronů v atomech).

Některé druhy, které binární systém rozlišuje jsou však v systému směrů považovány za ekvivalentní. Negace (změna všech − na + a naopak) nemění vlastnosti druhu.

 Instance S0(k):
    k=1:   -+
    k=2:   00
           -+ +-
           0- 0+ -0 +0
           -- ++

Např. Instance 00011 a 00111 patří v S(5) dvěma různým druhům.

V systému S(5) jsou −−−++ a −−+++, stejně jako −−−−− a +++++ téhož druhu.

Instance S(k):

    k=1: -+
    k=2: --  ++  -+ +-
    k=3: --- +++ --+ -+- +-- ++- +-+ -++

    k=4: 
    −−−− ++++
    −−−+ −−+− −+−− +−−− +++− ++−+ +−++ −+++
    −−++ −++− +−−+ ++−−
    −+−+ +−+−

V případě, kdy kromě možnosti + a –,

připustíme ještě (jako např. u nábojů částic) neutrální možnost 0, dostaneme další schemata:

Genetické struktury

Název "G-systémy" vznikl původně jako zkratka pojmenování "Genetické systémy". Struktury, které v těchto systémech vznikají, vykazují určité znaky dědičnosti. Vyšší systémy do sebe přebírají systémy nižší a to zároveň ve dvou rovinách – vnořováním (kapitola 8) a segmentací (kapitola 9). Tato analogie vybízí k porovnání G-systémů se stávajícími znalostmi o genetických strukturách.

Mendel, Johann Gregor

Mendel, Johann Gregor [mendl], 1822-1884, moravský přírodovědec německé národnosti. Po několika letech systematických pokusů s rostlinami vyjádřil pozorované vztahy matematicky. Tři Mendelovy zákony (O uniformitě míšenců, O štěpení znaků a O volné kombinovatelnosti vloh) tvoří základ moderní genetiky.

Dědičnost

Uvažujme 4 varianty spojení dvou možných prvků genetických vloh) A,a:

        a   A         0   1        a   A
    a  aa  aA     0  00  01     a  0   1 
    A  Aa  AA     1  10  11     A  2   3

Spojením aa, AA se říká homozygotní, spojením aA, Aa heterozygotní. Každé spojení představuje konfiguraci jednoho genu. Konfigurace je možné křížit, nové spojení obsahuje právě jeden prvek z obou konfigurací předků. Konfigurace všech genů vytvářejí tzv.genotyp.

Platí:

· Křížením homozygotů (bastardací) aa x AA mohou vzniknou jedině spojení aA nebo Aa, tj. heteozygoti ("nečistokrevní" jedinci, míšenci, bastardi). Všichni noví jedinci mají stejnou konfiguraci, jsou jednotní (uniformní).

· Křížením heterozygotů aA x aA může vzniknou kterékoliv spojení aa,aA,Aa,AA.

Dominatní a recesivní prvky

Prvek A je dominantní, pokud ovládá existující spojení a rozhoduje o jeho projevu; prvek a, který je 'slabší' než A, se říká recesivní Při křížení heterozygotů utvoří možná spojení prvků A,a 2 skupiny:

· aA,Aa,AA - mají vlastnosti určené prvkem A

· aa - má vlastnosti určené prvkem a

Vlastnosti určené prvkem a se v případě dominantního prvku A projevují tedy v průměru u 1/4 ze všech potomků.

Dominance a intermedierita

Pokud ani jeden z prvků nepřevládá, mluví se o tzv.intermedieritě (neúplné dominanci).

  Dominance:    Intermedierita:   
  Konfigurace Projev   Konfigurace Projev  
    00  0        00   0
   ─────────    ──────────
    01           01   1
    10  1        10
    11           ──────────
                 11   2

Projevy dominance genů připomínají matematické struktury nazývané ideály:

Představme si množinu prvků G, v němž se nachází podmnožina dominantních prvků D, přičemž je možné křížit každý prvek s každým. Pokud při křížení libovolného dεD a gεG vznikne potomek patřící D, nazývá se množina D ideál. Obdobné "dominantní" chování má nula vzhledem k násobení.

Křížení dvojice genů

Potomek, u něhož se pozoruje závislost na 2 (resp. 3,...) prvcích se nazývá dvojnásobný (resp. trojnásobný,...) míšenec - dihybrid (trihybrid,...).
Mějme nyní 2 geny s možnými prvky a,A,b,B.
Na prvních dvou pozicích zapíšeme první gen, a dalších dvou druhý gen. Malá písmena nahradíme nulami, velká jedničkami, např: aaBb = 0010 AaBB = 1011. Možné varianty spojení (vpravo se zápisem binárních čísel v desítkové soustavě):

Morgan Thomas Hunt

Morgan Thomas Hunt [], 1866-1945, americký zoolog a genetik. Mendelovy zákony doplnil o další, které vysvětlují funkce chromozómů při dědičnosti: 1/ Geny v chromozómech jsou uspořádány lineárně, 2/ Počet vazbových skupin je roven počtu párů chromozómů.

Pokusy ukázaly, že pokud počet potomků s konfiguracemi z množiny {1,2,4,8,7,14,13,11} je t, pak počet zbývajících {0,5,10,15},{3,6,12,9} je úměrný t² nebo 1.

Rozlišují se dva případy: 1/CIS (párování) a 2/ TRANS (odpuzování):

Dominantní dvojice genů

Když A,B jsou dominantní tvoří konfigurace čtyři skupiny:

Rozložení počtu potomků ve skupinách (ab:aB:Ab:AB) odpovídá experimentálním výsledkům. Např. pro CIS (t=7) 49:15:15:177, pro TRANS (t=127) 1:16383:16383:32769 [Hončariv].

Rozčlenění G-systému

Označme nyní spojení aa=bb=0, aA=bB=1, Aa=Bb=2 a AA=BB=3. Např. aaBb = 02, AaBB = 23, .... U míšenců existují kombinace:

k=2 (dihybrid), G(4,2) k=3 (trihybrid), G(4,3)