Hudební teorie - Energie

Micka Josef
Micka Josef , 1903-1993, český houslista, houslový pedagog a hudební teoretik, profesor houslové hry na Akademii múzických umění. V stručném pojednání o hudební dynamice naznačil nejobecnější (energetické) principy, které ovládají vnímání hudebních skladeb. Vysvětlil, kdy bývá oprávněné zesílení (crescendo) a kdy zeslabení (decrescendo) a pokusil se o rekonstrukci dynamických znamének u skladeb bez označení (Bachových fug,...).

Každý hudební prvek potřebuje k svému uskutečnění určité množství energie: vyšší tóny, pohyblivé a nepravidelné rytmy, dizonantní souzvuky, ... spotřebovávají více energie a vyžadují tak více energie od svého zdroje.

Interakce tónů

Energie harmonického kmitání je přímo úměrná amplitudě a frekvenci. Vyšší tóny vyžadují proto vyšší energii než nižší. Jsou-li však všechny tóny tvořeny interpretem se stejnou energií, pak nutně (podle J.Micky) nižší tóny (tj. s nižší frekvencí) vyzní z vyšší amplitudou, tedy silněji.

Energetická pásma

Nechť energetické pásmo je nositelem energie příslušející dané frekvenci. Předpokládejme, že tato energie nezaniká současně s dozněním tónu a přetrvává ve formě psycho-akustické. Déle znějící tóny přivádí do pásma více energie než tóny kratší. Energie zůstává v pásmu, dokud není odčerpána vnějšími silami. Analogicky s obdobnými fyzikálními jevy budeme předpokládat působení těchto vnější sil:

Odpor prostředí: způsobuje postupnou ztrátu energie pásma v čase.

Interakce mezi pásmy ( poli pásem): přerozdělují a spotřebovávají energie pásem.

Časovou ztrátu můžeme předpokládat např.ve tvaru

  E = E0 /exp(kt) 

Janáček Leoš
Janáček Leoš , 1854-1928, český skladatel a hudební teoretik. Zabýval se lidovou tvořivostí, vytvořil osobitý styl využívající lidových nápěvných prvků. Ve snaze vystihnou své hudební představy co nejvýstižněji, zavedl řadu zvláštních pojmů (pacitový tón, spletna, sčasovka,...).

kde t je čas a k nějaká konstanta (K.Asherov).

Základní pásmo

Pásmo, které je v daném časovém okamžiku nositelem největší energie nazýváme základní pásmo. Relativní charakteristiku vyjadřující poměrnou míru energie v pásmu nazveme základnost.

Tón o výšce v, hlasitosti h a délce d se zdá dodávat do pásma energii E úměrnou podle vztahu:

  E=d∙(h/v) 

Základnost tónu: - závisí do značné míry na struktuře souzvuku.

Spletna

V Janáčkově teorii harmonických spojů hraje významnou roli tzv. spletna. Spletnu tvoří vztahy mezi tóny, které vznikají v okamžiku, kdy původní (pacitový) souzvuk zaniká a nastupuje nový (pocitový). Podle typu spletny L.Janáček rozlišil tři hlavní typy harmonických spojů: "spoj usmíření" (půltónové rozvedení), "spoj záměnou" (kvintový vztah).

Janeček Karel
Janeček Karel , 1903-1974, český hudební teoretik a skladatel (tvůrce klavírní, komorní, vokální i orchestrální hudby). Jeden z největších českých hudebních teoretiků, systematik. Zabýval se teorií skladby a harmonií hudby, klasickou i moderní. Systematicky vypsal všechny možné souzvuky 12-ti tónové soustavy a ohodnotil je charakteristikami. Věnoval se hudební tektonice, hudebním formám, nauce o melodii, analýze hudebních skladeb a také otázkám kompoziční představivosti, talentu,... Myšlenky svých předchůdců zobecnil a přesněji formuloval, principy dokládal úkázkami z hudebních děl.

Imaginární tóny

Janáčkovy úvahy o spletně přeformuloval prof. Karel Janeček do teorie imaginárních tónů, viz Základy moderní harmonie []. K.Janeček rozlišuje harmonické a tonální imaginarní tóny, my si nyní povšimneme jen těch prvních. Harmonické imaginární tóny "zní" po ukončení reálných tónů. Stejně jako reálné tóny a spolu s nimi vytvářejí harmonické struktury. Imaginární tóny zní tak dlouho, dokud mají dostatek energie. Každý harmonický imaginární tón může být zrušen nějakým reálným tónem, přičemž konsonantní intervaly a tritonus ruší imaginarní tóny pomalu, celé tóny normálně a půltóny rychle. K.Janeček demonstruje teorii na několika příkladech a vyjasňuje některé zákonitosti klasické harmonie. Pomocí teorie imaginárních tónů definuje také princip čisté tóniky.

Typy interakcí

Jednotlivé tóny souzvuku nemá význam skládat v jedno vlnění - člověk je vnímá samostatně.

To v čem se souznění liší od souhrnu tónů jsou vazby, tj. vztahy tónů, interakce pásem příslušejících tónům,...

1.Rezonance mezi pásmy, jimž odpovídající frekvence jsou přibližně v poměru malých celých čísel.
 m_mcont.jpg

Jedno z pásem získává část potenciální energie pásma druhého. Množství předávané energie nazýváme spojitost vazby.

2.Reaktivnost mezi poli nejbližších pásem. Energie pásem odčerpává síla, která má maximum v určité malé vzdálenosti dvou pásem. (připomíná Newtonovu či Coulombovu sílu).
 m_mimpls.jpg

Vazebnou (kinetickou) energii, která se vybíjí interakcí pásem nazýváme impulz vazby.

Při interakci pásem vznikají vazby, které odčerpávají část energie pásem. Nechť např. harmonická vazba r12 mezi pásmy p1 a p2 zprostředkovává takovou interakci. Ke své existenci potřebuje energii Ev, jíž nemůže čerpat odjinud, než právě z pásem p1 a p2. Potenciální energie pásem Ep se postupně mění ve vazebnou (kinetickou) energii Ev.

Spotřeba energie ve vazbě závisí na typu vazby, především na velikosti hudebního intervalu. Předpokládáme, že dochází ke dvěma základním dějům. Podle nich rozlišujeme dva typy interakcí.

Zachování energie

Mějme dvě pásma s počáteční energií E1=E2=E(0). Nechť c(s) je spojitost vazby a i(s) impuls vazby, pro formální interval s.

Vazba spojitosti energii přenáší, tedy energie se zachovává:

Joule James Prescott
Joule James Prescott [džúl], 1818-1889, anglický fyzik, jeden z objevitelů zákona zachování energie.

  E1 = E(1–c)   E2 = E(1+c)

  E1 + E2 = 2E  

Vazba impulzu energii spotřebovává, energie klesá:

  E1 = E(1–i/2)  E2 = E(1+i/2)

  E1 + E2 = 2E – i  

(K.Asherov)

Impulz

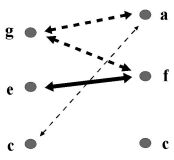m_harconi.jpg Kinetickou energii, která se vybíjí interakcí (blízkých) pásem nazýváme impulz vazby. Největší hodnoty impulzu jsou spojeny s nejmenšími intervaly.
Směr působení impulzu nezávisí na orientaci vazby; hodnota impulzu je vždy kladná.

Princip impulzu byl zaveden do hudební praxe dávno před principem spojitosti. Ale v hudební teorii zůstával téměř nepovšimnut.
Ve 20-tém století hudební teoretikové poukázaly na jeho existenci v několika nezávislých studiích:

L.Janáček spojem usmíření

A.Schőnberg ekonomií hudebního pohybu

K.Janeček teorií imaginárních tónů.

K.Risinger 2.principem funkčního vztahu.


Impulz je zdroj hudebního pohybu a hlavní faktor působící na naše city; přináší barvu a hustotu akordů, mění je v chaotické a disonantní. V polyfonii impulz zajišťuje ekonomii pohybu hlasů.

Impulz je výsledkem energetických interakcí pásem; je to energie spotřebovaná ve vazbách.


Spojitost

Vazba má jistou spojitost jestliže jí odpovídající pásma rezonují. Největší spojitost ve formálním systému nastává v případě poměrů 3:2, 5:4 a z nich odvozených (3:4,5:8). Spojitost budeme označovat písmenem c (angl.spojitost=continuity).

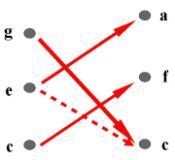m_harconc.jpg Idea spojitosti není nová. Stará čínská teorie říká, že každý tón dává vzniknout jinému tónu - čisté kvintě. J.P.Rameau považoval kvintu za přírodou daný interval přičemž vrchní kvintový tón (g) se na konci skladby vrací do svého zdroje (c). Podle jeho teorie fundamentálního basu vytvářejí smysluplné akordické sledy zejména souzvuky v kvintových vzdálenostech.

Spojitost najdeme také v úvahách dalších teoretiků:

v spoji záměnnou L.Janáček

v principu alikvotní řady L.Bardose

v 1.principu funkčního vztahu K.Risingera

Rameau Jean Philippe
Rameau Jean Philippe [ramo], 1683-1764, francouzský skladatel a hudební teoretik považovaný za zakladatele klasické harmonie. Harmonické jevy (terciovou výstavbu, autentický závěr,...) vysvětluje pomocí řady alikvotních tónů a rezonance. Hudba je založena na přibližnosti. Základem kvintakordu je nejspodnější tón a vztahy souzvuků jsou určeny poměrem jejich základních tónů. Položil základní kameny teorii tonality a diatonické modulaci. Melodie musí korespondovat s harmonií.


Harmonie s vazbami spojitosti je klidná a konsonantní. Hudební proud plyne plynule, bez zlomů. Kladná spojitost zdůrazňuje nový obsah.

Směr spojitosti

Spojitost závisí na směru působení. Podle směru vazeb spojitosti rozlišíme tzv. směr spojitosti. Spojitost je kladná nebo záporná. Podle toho je směr spojitosti přímý nebo protisměrný. Spojitost c má směr s=sign(c).

Spojitost od frekvence f1 k f2 je kladná, když odpovídající poměr f1/f2 má větší prvočíselné charakteristiky v čitateli než ve jmenovateli. Např. 3/2 (nebo 3/4) stejně jako 5/4 (nebo 5/8) má kladnou spojitost.

Znázornění charakteristik

Souřadná soustava - spojitost na vodorovné ose, impulz na svislé ose. 

    impulse (+)
                   c#
                   d
                   d#
                   e
                   f#
    continuity(–)  g  e ß  c à g# f continuity(+) 
                   g#
                   a
                   b
                   h

              identita 
                 |prima 
                 | 
                 |půltón 
                 | 
                 | 
                 |celý tón 
                 | 
              impulz 
                 | 
                 | .. 
                 | 
                 | .. 
                 | ... velká tercie - kvinta - oktáva 
                 |triton 
                 +---------- spojitost ------------------ identita

Maximální impulz i maximální spojitost konvergují do (oktávové) identity (tj. do primy resp.oktávy).

Za příčinou interakcí

Energetická pásma

Díky setrvačnost může basiální membrána dokázat udržet na určitý čas energii.

Stejně jako máme  visuální residua z delšího pozorování barevných objektů, můžeme mít i sluchová residua po poslouchání  jednotlivých frekvencí zvuku.

Spojitost

Přenos energie z jednoho tělesa na druhé se pozoruje fyzikálně při jevu zvaném

rezonance, při studiu vynucených kmitů.  Těleso s určitým vlastním kmitočtem se rozkmitá, pokud je mu těleso jiné s blízkým kmitočtem schopné energii předat. Takový jev nastává i např. při rozkladu složeného zvuku do harmonických složek pomocí rezonátorů.

Mechanizmus přenosu energie nemusí být vázán na sdílení energie svrchních tónů. Interakce vznikající na basiální membráně mohou interně pohlcovat či uvolňovat energii  a vytvářet určité energetické vztahy (spojitost)

Jestliže membrána vibruje působením  tónu A a je uveden tón B, není možné, že tón B pomůže membráně vibrovat nebo naopak že membrána pomůže vibrovat tomuto tónu?

Impulz

Soudržnost basiální membrány může být příčinou nemožnosti přijmout dvě nepatrně odlišné vlny. Existuje limit, minimální nutný rozdíl, který implikuje pozorované vztahy v chování blízkých tónů  (impulz)


Charakteristiky intervalů

Boltzmann Ludwig Eduard
Boltzmann Ludwig Eduard [bolcman], 1844-1906, rakouský fyzik, zakladatel kinetické teorie plynů a statistické fyziky, spoluobjevitel záření černého tělesa. 

Odhad hodnot charakteristik

Hmotnosti a rychlosti jednotlivých molekul vzduchu se v celku, který vyplňuje jistý objem,  projevují jako tlak a teplota. Obdobně je to s charakteristikami harmonických vazeb. Součet působení jednotlivých vazeb dává výsledné působení. Tlak a teplotu vzduchu můžeme snadno změřit, ale posoudit spojitost harmonického proudu neumíme. Celkovou hodnotu spojitosti musíme  odvodit z dílčích hodnot spojitostí  jednotlivých vazeb.

Obdobným způsobem se ve fyzice  odvozuje celá řada hodnot (např. sílu působící mezi Sluncem a některou z planet můžeme jedině spočítat, ne přímo změřit…).

Interval

–5

–4

–3

–2

–1

0

1

2

3

4

5

6

Spojitost

–c1

+c2

0

0

0

0

0

0

0

–c2

+c1

0

Impulz

+i5

+i4

+i3

+i2

+i1

0

+i1

+i2

+i3

+i4

+i5

0

V následujících odstavcích se budeme zabývat možnostmi stanovení dílčích charakteristik.

Vazby odpovídající intervalům 12-tónové soustavy ohodnotíme charakteristikou spojitosti a impulzu. Na základě odvozených hodnot se pokusíme zobecnit charakteristiky pro všechny formální soustavy.

Bez znalosti podstaty interakcí mezi pásmy není ale možné odvodit přesné hodnoty. Neznáme žádnou metodu, jak základní charakteristiky (spojitost, impuls) ani odvozené (entropie,..) fyzikálně měřit. Jediným zdrojem jsou známé základní tóny, [9], a různé míry konsonance, [6], [9], vybraných souzvuků. Podle nich odhadneme určité hodnoty. Na nich pak budeme později demonstrovat podstatu zamýšlených vztahů.

Impuls

Odhad hodnot impulzu

Impulz I mezi dvěma pásmy je funkcí energií E1, E2 a formálního intervalu s. Tóny jsou jako tělesa s gravitačními nebo elektro-magnetickými poli:

  I = f(E1,E2,s) = E1∙E2/g(s)  

m_impuls.jpg Pásma silně reagují, jestliže s je malé. V nejjednodušším případě, kdy E1=E2=1, impulz závisí jen na rozměru formálního intervalu s: I = f(s).
Působení impulzu nezávisí na směru vazby, tedy impulz je vždy kladný.

Největší impulz I , předpokládáme postupně u intervalu půltónu i1, celého tónu i2 a malé tercie i3. Impulzy dalších intervalů i4, i5 se zdají být zanedbatelné. Ve vzdálenosti mediánu soustavy (μ=k div 2) je předpokládán nulový impulz.

Interval

–5

–4

–3

–2

–1

0

1

2

3

4

5

6

Impulz

i5

i4

i3

i2

i1

0

i1

i2

i3

i4

i5

0

Rozložení energie

Uvažujme dva tóny A,B  s frekvencemi fA a fB, jejichž vzdálenost v oktávách je x (K.Asherov). Předpokládejme, že mezi A a B vznikne síla F(x) = –1/x², která brání jejich současnému znění. Integrací F(x)dx dostaneme energii E(x) = E0 + 1/x. Jestliže x=1/2, tak E = E0 – 2 = 0 a E(x) = 1/x – 2. Pro vzdálenost v půltónech s je x = s/12 a E(s) = 12/s – 2. Energie půltónu E(1) = 12/1 – 2 = 10 a impuls je úměrný této energii i(s) ~ E(s), tedy pro kvadratické rozložení síly vychází: 

  i(s) = i(1)/E(1)∙(12/s –2)  

kde E(1)=10.

Stejně můžeme postupovat i pro kubické či jiné hypotetické rozložení. Pro kubické rozložení přitaživosti je

  i(s) = i(1)/E(1)∙(288/s² –8)  

kde E(1)=280.


Impuls pod hranicí půltónu

Pokud je impuls nepřímo úměrný vydálenosti x [oktáv], tj. i(x)~1/x, pak pro x >> 1 je i = 0. Někde okolo hranice půltónu dosahuje impuls maxima. Pro x=0 se ydá ale být opět i=0, tj. impuls unizona je nulový. V intervalu půltónu 0 à 1 musí podle toho růst impuls k maximu.

Zavedeme exponenciální funkci i(s) = p∙sn/eqs např. pro n=2. Z derivace zjistíme maximum a pak můžeme zvolit konstanty p, q tak, aby extrém byl tam, kde má být.

Takovou funkcí je např.

  i(s) = p∙(s²/e²s)  

kde p=88.7.

Hodnoty impulsu 

s    1/s    1/s2   s2/e2s 
-------------------------- 
1/2 26.40   49.03   8.15 
 1  12.00   12.00  12.00 
 2   4.80    2.74   6.50 
 3   2.40    1.03   1.98 
 4   1.20    0.43   0.48  
 5   0.48    0.15   0.10 
 6   0.00    0.00   0.02

Definujme hodnotu impulzu půltónu, např. i(1) = 12 a spočítejme výsledné hodnoty. Budeme uvažovat funkce:

 i(s) = 12/10  ∙(12/s –2)

 i(s) = 12/280 ∙(288/s² –8)

 i(s) = 88.7   ∙(s²/e²s)

Ztráta energie

Vazby mezi tóny, které nerezonují nemají důvod si předávat energii. Mohly by proto např. jen vyrovnávat energie tónů. Zdá se ale že spíše energii tónů odčerpávají. Pokusíme se hledat argumenty pro toto tvrzení. Uvažujme, že každý zvuk, který můžeme slyšet, musí mít svůj vlastní zdroj energie. Když posloucháme dva oddělené tóny v konsonantním intervalu nebo v takové vzdálenosti, že se příliš neovlivňují, slyšíme jen tyto tóny. Když ale zahrajeme půltón, slyšíme tóny a něco navíc (dizonanci...). Co je to? (rázy, šum,..?) Tento efekt musí stát nějakou energii (např. nové tóny, které vznikají dílem rázů musí mít svoji energii) a tato energie musí vycházet z nějakého energetického zdroje. Jediným zdrojem energie jsou však hrané tóny.

Imaginární tóny

Pokračujme nyní v Janečkově teorii imaginárních tónů. Nechť zazní reálný tón g. V okamžiku, kdy přestane znít, mění se na imaginární tón. Tento imaginární tón (G) může být zrušen:   1/ tónem F# nebo G# nebo 2/ tónem F.

Někdy také (podle K,Janečka) může být zrušen: 3/ tónem A, to ale jedině v případě, že jsou splněny následující podmínky:

imaginární tón není zdůrazněn

tón A je delší nebo významější

tón G není předcházen tónem F nebo F#

A dále, jestliže tón G zní zároveň s F# (přípustné jsou i jiné oktávy), pak tón F tón G nezruší. V tomto případě je tón F# nazýván "kritický protirušivý tón" (tónu G).

Za předpokladu, že impulz spotřebovává energii vazeb, jsou body 1-3 pochopitelné. K vysvětlení rozdílu mezi tónem G a A si musíme navíc vypomoci Mickovým zdůvodněním výraznějších basových tónů (v kapitole Hudební energie).

Kritický protirušivý tón dokazuje, že impuls půltónu je větší než impuls celého tónu.

Závislost impulsu na výšce tónů

Závisí impuls na kmitočtu? Lidský sluch nerozlišuje půltóny v nižších oktávách stejně jako ve vyšších. Rázy mezi f1 = 220 HZ a f2 = 224 Hz f = f2 – f1 = 4 Hz. Ale dvě oktávy výše mezi f1 = 880 HZ a f2 = 896 Hz to je 16 Hz. Menší výškové posuny jsou více slyšitelné ve vyšších registrech.

Matice impulzu

Každé jednotlivé harmonické vazbě formálního soustavy je přiřazena hodnota impulzu. Souhrn všech hodnot vytváří matici impulzu. 

     c  c# d  d# e  f  f# g  g# a  a# h
 
c    0  i1 i2 i3 0  0  0  0  0  i3 i2 i1 
c#   i1 0  i1 i2 i3 0  0  0  0  0  i3 i2 
d    i2 i1 0  i1 i2 1  0  0  0  0  0  i3 
d#   i3 i2 i1 0  i1 i2 i3 0  0  0  0  0 
e    0  i3 i2 i1 0  i1 i2 i3 0  0  0  0 
f    0  0  i3 i2 i1 0  i1 i2 i3 0  0  0 
f#   0  0  0  i3 i2 i1 0  i1 i2 i3 0  0 
g    0  0  0  0  i3 i2 i1 0  i1 i2 i3 0 
g#   0  0  0  0  0  i3 i2 i1 0  i1 i2 i3 
a    i3 0  0  0  0  0  i3 i2 i1 0  i1 i2 
a#   i2 i3 0  0  0  0  0  i3 i2 i1 0  i1 
h    i1 i2 i3 0  0  0  0  0  i3 i2 i1 0

Spojitost

Odhad hodnot spojitosti

m_contin.jpg Spojitost c udává množství energie tekoucí ve vazbě. Je funkcí energií pásem E1,E2 a formálního intervalu s. V nejjednodušším případě E1=E2=1 spojitost závisí jen na formálním intervalu s: c = C(s).

Největší spojitost C uvažujeme u intervalů čisté kvinty (rezonance 3:2) a velké tercie(5:4).
Interval čisté kvarty (4:3) a malé sexty(8:5) je formálně od uvedených intervalů nerozlišitelný.
Spojitost záleží na směru působení.
Sestupná kvinta C(–7)= C(+5)=+c1 má kladnou spojitost. Stejně tak i sestupná velká tercie C(–4)=C(+8)=+c2. Spojitosti ostatních intervalů zanedbáváme.

Interval

–5

–4

–3

–2

–1

0

1

2

3

4

5

6

Spojitost

-c1

+c2

0

0

0

0

0

0

0

-c2

+c1

0

Podmínky základního tónu 
  Va = c(e->a) + c(c->a) - (i(e↔a)+i(c↔a))/2 
  Vc = c(e->c) + c(a->c) - (i(e↔c)+i(a↔c))/2 
  Ve = c(a->e) + c(c->e) - (i(a↔e)+i(c↔e))/2

Přibližné hodnoty charakteristik můžeme získat i bez měřících přístrojů. Nechme zaznít trojzvuk A moll (a,c,e) a předpokládejme, že většina posluchačů označí za základní tón a (bez ohledu na oktávové umístění). Odtud můžeme soudit, že existuje určitý přesun energie k tónu a.Pomocí hodnot energií Va, Vc, Ve zapíšeme podmínku pro přesun energie k tónu a pomocí dvou nerovností: Va >Vc, Va>Ve, tj. Va =max(Va,Vc,Ve).

Risingerovy podmínky

K. Risinger' uvádí podmínky k určení základních tónů akordů []. Následující souzvuky mají základní tón C bez ohledu na převraty (přeskupení tónů) za podmínky, že tóny jsou co nejblíže k sobě (tj. nejsou příliš ovlivněny oktávovými pozicemi) :

Trojzvuky: C-D-Eb, C-D-E, C-Es-G, C-E-G, C-F#-G, C-E-B, C-G-B, C-G-H

Čtyřzvuky: C-D-Eb-E, C-Eb-E-G, C-E-F#-G, C-Eb-G-H, C-E-G-B, C-G-B-

H,C-D-E-G.

Pětizvuky1: C-D-Eb-E-G, C-Eb-E-F#-G, C-E-F#-G-B 



 Hodnota spojitocti c1. - Z vazeb v souzvuku C-Eb-G-H plyne:
       V(C) = c1–(i1+i3+i5)/2 
       V(Eb) = c2–c2–(i3+i4+i4)/2 
   where V(C)>V(Eb), i.e. c1>(i1+i5)/2–i4.

 Hodnota spojitocti c2. - Z vazeb v souzvuku C-G-B-H plyne:
       V(C) = c1–(i1+i2+i5)/2 
       V(G) = c2–c1–(i3+i4+i5)/2
   where V(C)>V(G) i.e. 2c1–c2>(i1+i2–i3–i4)/2
Některé ze souzvuků nevypovídají příliš mnoho. Jiné jsou ale zajímavé, povšimneme si dvou z nich:. C-Eb-G-H a C-G-B-H. Označme hodnoty impulzu i1,i2,i3,i4,i5 a hodnoty spojitosti c1, c2 (např. c1:g => c, c2:e =>c).

Pro exponenciální rozložení (viz výše odstavec Hodnoty impulzu) s přibližnými hodnotami i1=12, i2=6.5, i3=2,  i4=0.5,  i5=i6=0  vychází c1>12/2-0.5 tj. c1> 5.5.

Pro c1= 6 je 12–c2>(i1+i2–i3–i4)/2, a tedy c2 <12-(12+6.5-2-0.5)/2 tj. c2 < 4.

Z hodnot impulzu a pozorovaných základních tónů vybraných souzvuků jsme odvodili neznámé hodnoty spojitosti.  Přitom se potvrzuje základní předpoklad, že spojitost (sestupné) velké tercie (c2) je menší  než (sestupné) čisté kvinty (c1).

i1

i2

i3

i4

c1

c2

ostatní

12

6.5

2

0.5

6

3

0

K zjednodušení dalších výpočtů použijeme přibližných hodnot.



Sdílení pásem

Barvy zvuku si - na rozdíl od světla - při mísení zachovávají do určité míry individuální charakter.

Předpokládejme rovnoměrné rozložení intenzit alikvotních tónů a přiřadit tytéž alikvotní tóny (různých akordických tónů) do stejných pásem. Např. alikvot e obou tónů a, c (v akordu f,a,c) je ve stejném pásmu.

Když všechny alikvotní tóny jsou jen v pásmech, informace, který tón má které alikvoty (a s jakou intenzitou) je ztracena. (Slyšíme jen barvu tónů). Některé tóny pomáhají jiným tónům znít. V našem příkladu c může využít část celkové energie tónu a (s ohledem na pásmo e).



Závislost spojitosti na výšce tónů

Formální soustava nerozlišuje oktávy tónů a tedy spojitost od c2 ke g2 (7 půltónů) je stejná jako od c2 ke g1 (–5 půltónů). A také impulz mezi c1 a c#1 (1 půltón) je stejný jako mezi c1 a c#2 (13 půltónů). S oktávou se zachází stejně jako s unisonem.

Tím dochází k jistému zkreslení, charakteristiky závisí také na oktávové poloze - je proto potřebné formální hodnoty upravit.

Matice spojitosti

Každé jednotlivé harmonické vazbě formálního soustavy je přiřazena hodnota spojitosti. Souhrn všech hodnot vytváří matici spojitosti. 

     c   c#  d   d#  e   f   f#  g   g#  a   a#  h
 
c    0   0   0   0  -c2 +c1  0  -c1 +c2  0   0   0 
c#   0   0   0   0   0  -c2 +c1  0  -c1 +c2  0   0 
d    0   0   0   0   0   0  -c2 +c1  0  -c1 +c2  0 
d#   0   0   0   0   0   0   0  -c2 +c1  0  -c1 +c2 
e  +c2   0   0   0   0   0   0   0  -c2 +c1  0  -c1 
f  -c1  +c2  0   0   0   0   0   0   0  -c2 +c1  0 
f#   0  -c1 +c2  0   0   0   0   0   0   0  -c2 +c1 
g  +c1   0  -c1 +c2  0   0   0   0   0   0   0  -c2 
g# -c2  +c1  0  -c1 +c2  0   0   0   0   0   0   0 
a   0   -c2 +c1  0  -c1 +c2  0   0   0   0   0   0 
a#  0    0  -c2 +c1  0  -c1 +c2  0   0   0   0   0 
h   0    0   0  -c2  +c1 0  -c1+c2   0   0   0   0

Charakteristiky modalit

-

c

d

e

f

g

a

h

c

0

+2

+4

+5

–5

–3

–1

d

–2

0

+2

+3

+5

–5

–3

e

–4

–2

0

+1

+3

+5

–5

f

–5

–3

–1

0

+2

+4

+6

g

+5

–5

–3

–2

0

+2

+4

a

+3

+5

–5

–4

–2

0

+2

h

+1

+3

+5

+6

–4

–2

0

Spojitost modality

Na příkladu přirozené modality [c,d,e,f,g,a,h] ukážeme výpočet spojitosti modality.V tabulce intervalů je číslo 5 (+5 nebo –5) v každém řádku. Každý tón přirozené modality má kvintový poměr k alespoň jednomu jinému tónu.

c

d

e

f

g

a

h

K

2

2

2

1

2

2

1

T

1

0

1

1

1

1

1

Hodnota spojitosti je funkcí kvintových intervalů a intervalů velké tercie.

Celkem je v přirozené modalitě N=7²=49 intervalů, z čehož je 12 kvint (K) se spojitostí c1 a 6 velkých tercií (T) o spojitosti c2.

K vyčíslení konkrétních příkladů použijeme hodnot c1=2,c2=1. Celková (absolutní) průměrná spojitost přirozené modality je ∑s=12*c1+6*c2=30.

Pro srovnání spojitost cikánské modality je 8*c1+10*c2=26, spojitost harmonické moll i podhalské lidové činí (8*c1+8*c2)=24.

Relativní spojitost vzhledem ke všem vazbám činí v přirozené heptatonice s=∑s/N= 30/49=0.61. Relativní spojitost slouží k porovnání modalit s různými počty tónů.

Např. přirozená pentatonika 2322(3) má celkovou spojitost 8*c1+2*c2=18 a relativní spojitost s=∑s/N= 18/25=0.72. Přirozená pentatonika má tedy relativně vyšší spojitost než přirozená heptatonika.

Spojitost vztažená k tónu

K

T

Spojitost

Spojitost tónu

c

2

1

2c1+c2

5/30=16.67%

d

2

0

2c1

4/30=13.33%

e

2

1

2c1+c2

5/30=16.67%

f

1

1

c1+c2

3/30=10%

g

2

1

2c1+c2

5/30=16.67%

a

2

1

2c1+c2

5/30=16.67%

h

1

1

c1+c2

3/30=10%

Spojitostí vztaženou k tónu rozumíme hodnotu (v procentech), kolik daný tón přispívá k celkové spojitosti modality.

V přirozené modalitě přispívají k spojitosti nejvíce tóny

c,e,g,a  (jsou spojeny s ostatními dvěma kvintami a  jednou v.tercií)

– pokrývají 2/3  celkové spojitosti.

V přirozené modalitě se stabilizovaly postupně dvě tóniny – durová a aiolská moll.

Tónikou (viz Harmonické funkce) durové tóniny je souzvuk [c,e,g] , tónikou mollové tóniny souzvuk [a,c,e]. V novější hudbě se objevuje jako tónika i celý čtyřzvuk [c,e,g,a].

Srovnání s rozložením spojitostí v jiných modalitách:

Přirozená

Podhalská

Harm. moll

Cikánská

Schéma

221222(1)

221212(2)

212213(1)

213113(1)

Modalita

cdefgah

cdefgg#a#

ahcdefg#

ahcd#efg#

∑

5 4 5 3 5 5 3 

6 3 2 4 4 2 3

5 2 4 2 6 3 2

3 3 4 3 6 3 4

Maxima

c,e,g,a

c,f,g

a,c,e

c,e,g#

Cikánskou modalitu jsme zde uvedli ve tvaru, ve kterém se nejvíce blíží harmonické moll.

Vysoká spojitost tónu e se  zdá značit, že uvedený tvar nemusí být základní.

Obvykle bývají uváděny dva tvary: cikánská dur 131213(1) a cikánská moll 213113(1). Za základní tvar se pokládá indická bhairava 131213(1) (podle které se učí všechny ostatní transpozice). V provedení efg#ahcd#  je počáteční tón e tónem nejvyšší spojitosti.

Narušení tónu impulzem

m_potent.jpg Uvažujme nyní dále, že spojitost vztaženou k jednotlivým tónům ruší vazby impulzu.

Definujeme proto vazebné ovlivnění tónu vztahem

 b = f( |c|, i) 

kde b je vazebné ovlivnění,   |c|  absolutní hodnota spojitosti, i impulz a f nějaká funkce.

(Matice ovlivnění je funkcí matic spojitosti a impulzu  B = g(C,I)).

Uvažujme například následující hodnoty vazebných ovlivnění:

 Interval

–5

–4

–3

–2

–1

0

1

2

3

4

5

6

 Vazebné ovlivnění

+4

+2

–1

–1

–2

0

–2

–1

–1

+2

+4

0

-

c

d

e

f

g

a

h

∑

c

0

–1

+2

+4

+4

–1

–2

+6

d

–1

0

–1

–1

+4

+4

–1

+4

e

+2

–1

0

–2

–1

+4

+4

+6

f

+4

–1

–2

0

–1

+2

–2

0

g

+4

–1

–1

–1

0

–1

+2

+7

a

–1

+4

+4

+2

–1

0

–1

+7

h

–2

–1

+4

–2

+2

–1

0

0

Potenciál pásma

Součet vlivů b jednotlivých vazeb na daný tón (dané energetické pásmo) nazveme potenciálem tónu v modalitě (formálním potenciálem, F-potenciálem).

   U(i) = ∑b(hi,j)

kde h je formální interval a i,j ε (0,k–1), j!=i.Potenciál nezávisí na směru spojitosti. F-potenciál je součtem (viz poslední sloupec) B-ovlivnění (v řádcích):

m_pdiag.jpg Potenciály pásem přirozené modality:

U(g) = U(a) = 7.0 U(c) = U(e) = 6.0 U(d)  = 4.0 U(f) = U(h) = 0.0

Vidíme v podstatě týž výsledek, který jsme odvodili výše: tóny {c,e,g,a} mají největší největší F-potenciál.

Vliv uspořádanosti souznění

Kromě dílčích vlivů očekáváme u interakcí více než dvou pásem také vliv celkové entropie souznění. Lépe uspořádaná uskupení tónů (konsonance) ztrácí méně energie.

Nechť m je binární vektor modality a U matice potenciálů. Vektor představuje F-potenciály tónů modality.    u = m∙U

Potenciál

 Podle vazebných ovlivnění vyčíslíme formální potenciály jednotlivých pásem
(celkový formální potenciál v posledním sloupci je součtem dílčích B-ovlivnění v řádce).

-  potenciály ( tóny pevné, citlivé volné ... )

tóny - pevné ( c,e ) => tónika  - citlivé ( f,h ) - vázané ef, hc (Země,Měsíc)  - volné ( g,d,a )   tóny - klidné ( lze na nich zakončit melodii )      - neklidné ( nejvíce h , d )

Primární pásma

Z k-pásem formální soustavy vybereme jen p takových, která mají energie přímo od tónů (primary, P- pásma). Ostatní, vedlejší pásma (secondary, S-pásma) získají energii prostřednictvím vazeb. Vazby mezi pásmy P-P, P-S (S-P), S-S mají různý význam, nejdůležitější jsou pro nás vazby P-P.
Probíhá-li hudební fráze v jisté modalitě, zůstanou některá pásma po celou dobu bez příjmu energie, v důsledku přerozdělování energií však nikoli prázdná. Za předpokladu, že příjem energií do P-pásem je vyrovnaný, můžeme jen ze struktury modality odvodit některé charakteristiky.

Budeme-li uvažovat i spolupůsobení vedlejších pásem (vazby PS) získáme hodnoty: g,a: 7; c,e:6; d:4; f,h:0; f#,a#:–2; g#, d#, c#:–4. Vybraným souzvukm přirozené modality odpovídají následující formální potenciály: P( C) = P(Ami) = 6.33; P( Emi) = P( F) = 4.33; P( Dmi) = P(G) = 3.67; P( Hmi5–) = 1.33. Hodnoty jsou určeny na jeden tón, např. pro C: P(C)=(c, e, g) = [P(c)+ P(e)+ P(g)]/3 = (6+6+7)/3 = 6.33.  Mezi tzv. tonálními kostrami  uvedl  P.Panoff  strukturu 2212(5), tj.[c,d,e,f,g] a 2122(5), tj.[c,c#,d#,f,a#], obě nad základním tónem c. V první ze strukur má tón c skutečně vysoký potenciál (podle potenciálů tóny tvoří řadu c,g,d,f,e).  Ve druhé struktuře ale (podle naší definice potenciálu)  získává nadvládu tón f (tóny tvoří řadu  f,a#, d#,c,c#).

Sekundární pásma

Až dosud jsme uvažovali jen primární pásma, t.j. pásma korespondující s tóny modality. V následující tabulce počítáme také potenciály sekundárních pásem. 

 modalita: 1  0  1  0  1  1  0  1  0  1  0  1  | formální
 tóny:     c  c# d  d# e  f  f# g  g# a  a# h  | potenciál
  -----------------------------------------------------
    c      0    –1    +2 +4    +4    –1    –2  | +6    c
    c#    –2    –2    –1 +2    –2    +2    –1  | –4    c#
    d     –1     0    –1 –1    +4    +4    –1  | +4    d
    d#    –1    –2    –2 –1    +2    –2    +2  | –4    d#
    e     +2    –1     0 –2    –1    +4    +4  | +6    e
    f     +4    –1    –2  0    –1    +2    –2  |  0    f
    f#    –2    +2    –1 –2    –2    –1    +4  | –2    f#
    g     +4    +4    –1 –1     0    –1    +2  | +7    g
    g#    +2    –2    +2 –1    –2    –2    –1  | –4    g#
    a     –1    +4    +4 +2    –1     0    –1  | +7    a
    a#    –1    +2    –2 +4    –1    –2    –2  | –2    a#
    h     –2    –1    +4 –2    +2    –1     0  |  0    h

Potenciály všech pásem přirozené modality:

U(g) = U(a) = 7.0,  U(c) = U(e) = 6.0,  U(d)  = 4.0,

U(f) = U(h) = 0.0,  U(f#)= U(a#)=–2.0, U(c#)= U(d#)=U(g#)=–4.0

Objekt v kontextu

(Posloupnost objektů, Charakteristická rovnice, Hudební proud)

Posloupnost objektů

Mějme nějakou posloupnost objektů A,B,C..., které mají jisté přirozené vlastnosti (stavy) definované hodnotami vektorů a,b,c,...

Objekty jsou přizpůsobivé. Pod vlivem svého předchůdce změní objekt X svůj stav na x'. V našem příkladě nastane a,b',c',.... Má-li objekt dostatek času, konverguje zpět do svého přirozeného stavu. např. a,b',c' -> c.

Předpokládáme, že existují 2 procesy:

Charakteristická rovnice

Dosáhne-li objekt již svého přirozeného stavu, pak jej konvergence dále nemění:

 N * c = 1 * c.

Tato rovnice je specielním případem charakteristické rovnice:

  N*c = b *c, kde c je charakteristický vektor

a b charateristické číslo (b=1).

Hudební proud


Předložený návrh aplikujme na příkladě hudebního proudu.
Každý souzvuk má elementární vlastnosti (potenciály tónů, spojitost, impulz, ...),
a v důsledku i jisté konkrétní vlastnosti (sonantnost, rod, ...).
Všechny tyto vlastnosti se v kontextu mění.
Např. samotný souzvuk G vyzní jinak, než souzvuk G v posloupnosti F-F#-G.
Dojmu čistého G nabýváme až po jistém čase konvergence.