Harmonický proud
Harmonická kinetika se zabývá harmonickými spoji a jejich působením. Posloupnost harmonických spojů budeme nazývat harmonický proud.
Hostinský Otakar| Hostinský Otakar , 1847-1910, český estetik, historik, muzikolog a hudební teoretik. Zakladatel moderní české estetiky a hudební vědy, autor řady hudebních historických prací. Zdůrazňoval, že věda má postupovat od jednoduchého ke složitějšímu, např. trojzvuk tvoří 6 intervalových dvojic. Porozuměl barvě zvuku,obhajoval mediantní spoje, prováděl srovnávací analýzy variant písní. Hledal pravidla české hudební deklamace (přízvučnosti slabik). Zabýval se také teorií a dějinami výtvarného umění a teorií literatury. Programní hudbu považoval za složené umění. |
(Pojem dynamika byl již v hudbě zaveden -v souvislosti se zdůrazněním tónů a hlasitostí zvuku, jako protikladu hudební statiky se proto používá pojmu kinetika).
Harmonický spoj
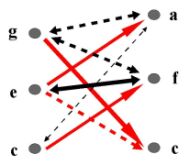
Harmonický spoj vzniká uvedením dvou tónových uskupení bezprostředně za sebou.
Tóny jsou nositely akustických kvalit a charakteristik (frekvence, amplitudy,lokace v čase...).
Z jejich vztahů odvozujeme další charakteristiky (spojitost, impulz,…), přitom za určující budeme považovat střední hodnoty charakteristik jednotlivých vazeb působících v daném časovém okamžiku.
Harmonické spoje působí obdobně, odpovídají-li si (kvalitou i kvantitou) jednotlivé vazby.
Více harmonických spojů za sebou vytváří harmonický proud.
Rozložení potenciálů v tónině určuje jisté hladiny pro jednotlivé
souzvuky. Vztahy mezi hladinami dávají vzniknout hudebnímu napětí,
které nutí harmonický proud k dalšímu pohybu.
Kontrasty napětí a uvolnění vznikají také v důsledku rozdílné sonantnosti (entropie) souzvuků. Harmonický spád (tendence) je ale určen jen umístění souzvuku v tónině, napětím (entropií) uvnitř souzvuku není ovlivněn.
Podle směru působení spojitosti rozlišujeme harmonický proud přímý (s kladnou spojitostí ke každému dalšímu souzvuk) a harmonický proud reverzní (se spojitostí zápornou).
Harmonický spoj je spojení dvou souzvuků. Každý tón prvního akordu je spojen s každým tónem druhého akordu.
Dlouho hudební teorie užívala jen vazeb mezi základními tóny akordů.
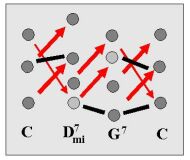 L.Janáček začal uvažovat vazby
ze všech tónů prvního akordu k základnímu tónu druhého akordu.
L.Janáček začal uvažovat vazby
ze všech tónů prvního akordu k základnímu tónu druhého akordu.
Harmonická fráze C-Dmi7-G7-C sestává ze 3 spojů.
C-Dmi7: Dmi7-G7: G7-C: c e g f a c d g h d f 2 –2 –5 d 0 –4 5 3 f 0 –4 5 2 g 0 –4 5 c –3 5 2 0 d –3 5 2 –1 e –3 5 2 a 6 2 –1 –3 h 5 1 –2 –5 c 5 1 –2 f 2 –2 –5 5 g
Kinetické charakteristiky akordů (potenciál,funkčnost,...) závisí také na modalitní struktuře …
Triviální spoje

Triviální harmonický spoj je navázání dvou identických uskupení. Harmonická statika je podmnožinou harmonické kinetiky: izolovaný akord může být nahlížen jako triviální harmonický spoj.
Sekvenční spoje
Harmonické spoje se zpravidla odehrávají v jedné určité modalitě. Sekvencí se rozumí takový postup určitého útvaru, při němž se samotný útvar (souzvuk) mění, ale zachovává (pokud možno) tvar. Podle vztahu k modalitě rozlišujeme: [Filip]
translace, tj. posuny útvaru v modalitě, např. C =>DmiàEmiàF
transpozice, tj. posuny v soustavě (vně modality), např. C=> C#à D
mutace (přehodnocení do jiné modality), např. CàDmiàEb.
Výčet vazeb
Pro vybrané spoje spočítáme počty vazeb s daným intervalem (–5..6).
Spoje identity|
0 |
1 |
–1 |
2 |
–2 |
3 |
–3 |
4 |
–4 |
5 |
–5 |
6 |
spoje |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
CC, AmiAmi |
|
3 |
0 |
0 |
0 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
2 |
Hmi5–Hmi5– |
Spoje s převahou spojitosti:
|
0 |
1 |
–1 |
2 |
–2 |
3 |
–3 |
4 |
–4 |
5 |
–5 |
6 |
spoje |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
CF, GC |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
EmiAmi, AmiDmi |
|
1 |
0 |
0 |
2 |
1 |
0 |
2 |
0 |
0 |
2 |
0 |
1 |
DmiG |
|
1 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
1 |
Hmi5–Emi |
|
1 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
1 |
FHmi5– |
Spoje s převahou impulzu:
|
0 |
1 |
–1 |
2 |
–2 |
3 |
–3 |
4 |
–4 |
5 |
–5 |
6 |
spoje |
|
0 |
2 |
0 |
1 |
2 |
0 |
0 |
0 |
1 |
2 |
0 |
1 |
EmiF |
|
0 |
1 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
CHmi5– , Hmi 5–Ami |
|
0 |
0 |
1 |
3 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
FG |
|
0 |
0 |
1 |
3 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
DmiEmi |
|
0 |
1 |
0 |
2 |
2 |
0 |
1 |
0 |
0 |
2 |
1 |
0 |
CDmi,GAmi |
| Volek Jaroslav , 1927-1989, český hudební vědec, hudební teoretik a estetik. Zabýval se filozofií a hudební teorií z obecného pohledu. Formuloval tzv. zodpovědnou vazbu, kterou tvoří v starší hudbě melodie, v hudbě novější harmonie. Podpořil Janáčkovu teorii harmonických spojů. Prosazoval začlenění mediant do systému harmonických funkcí. |
Medianty
“Mediantní” spoje durových a molových trojzvuků.
V prvním sloupci je počet společných tónů. Např. [c,e,g] a [a,c,e] mají 2
společné tóny {c,e}.
Počet vazeb pro interval (–5..6):
|
0 |
1 |
–1 |
2 |
–2 |
3 |
–3 |
4 |
–4 |
5 |
–5 |
6 |
spoj |
|
2 |
0 |
0 |
0 |
1 |
2 |
0 |
1 |
1 |
0 |
2 |
0 |
Ami-C |
|
2 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
2 |
2 |
0 |
0 |
Emi-C |
|
1 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
1 |
1 |
Ami-Cmi |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
3 |
1 |
0 |
0 |
Emi-Cmi |
|
1 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
1 |
1 |
A-C |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
3 |
1 |
0 |
0 |
E-C |
|
0 |
0 |
2 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
2 |
A-Cmi |
|
0 |
1 |
2 |
0 |
0 |
1 |
0 |
2 |
2 |
0 |
1 |
0 |
E-Cmi |
Mediantní spoje
- se dvěma společnými tóny (Ami-C,..,C-Emi) mají nejvyšší spojitost.
- s jedním společným tónem jsou stejnorodé (Ami-Cmi,..,C-E)
- bez společných tónů, tzv. chromatické medianty (A-Cmi,..,Cmi-E), mají nejvyšší impulz.
Charakteristiky
Míra spojení dvou souzvuků je určena celkovou hodnotou dané charakteristiky (spojitosti nebo impulsu).
Jestliže spoj dvou souzvuk (daný vektory u,v) má charakteristiku f (danou maticí F) pak f(u,v) = u∙F∙v = ∑∑F(hk,l)/(m∙n), kde hk,l je intervalová struktura, k=0..m–1, l=0..n–1, m,n jsou dimenze u,v.
Intervaly c e g --------- –3 5 2 a 5 1 –2 f 0 –4 5 c |
Spojitost: c e g ---------- 0 4 0 a 4 0 0 f 0 2 4 c |
Impulz: c e g ---------- 1 0 3 a 0 12 3 f 0 0 0 c |
| c(C-F)=(3∙4+2)/9=14/9=+1.56 | i(C-F)=(12+2∙3+1)/9= 19/9=2.11 |
Např. spojitost (impulz) harmonického spoje [C,F] je součinem: vektoru akordu C i.e.: u=[1,0,0,0,1,0,0,1,0,0,0,0]
matice spojitosti (impulzu) a vektoru akordu F: v= [1,0,0,0,0,1,0,0,0,1,0,0]
Vybrané spoje v přirozené 7-tónové modalitě 12-ti tónového systému (spoje konsonantních trojzvuků) mají následující hodnoty spojitosti a impulzu:
Vybrané spoje|
Harmonický spoj |
∑Spojitost |
∑Impulz |
øSpojitost |
øImpulz |
|
EmiAmi, GC, CF |
3c1+c2 |
i1+2i2+i3+i4 |
+2.33 |
3.06 |
|
EmiC, AmiF |
2c1+2c2 |
i1+2i3+2i4 |
+2.00 |
1.89 |
|
EmiF |
2c1+c2 |
2i1+3i2+i4 |
+1.67 |
4.89 |
|
Hmi5-Emi, FHmi5- |
2c1+c2 |
i1+2i2+i3+i4 |
+1.67 |
3.06 |
|
DmiG |
2c1 |
3i2+2i3 |
+1.33 |
2.61 |
|
CAmi, FDmi, GEmi |
2c1 |
i1+2i3+2i4 |
+1.33 |
1.89 |
|
Hmi5-C, AmiHmi5- |
c1+c2 |
2i 1+3i2+i4 |
+1.00 |
4.89 |
|
Hmi5-G, DmiHmi5- |
c1+c2 |
i2+3i3+i4 |
+1.00 |
1.44 |
|
GAmi, CDmi |
c1 |
i1+4i2+i3 |
+0.67 |
4.44 |
|
DmiEmi, FG |
0 |
i1+4i2+i3 |
0.00 |
4.44 |
|
AmiAmi, CC |
0 |
2i3+2i4 |
0.00 |
0.56 |
|
Hmi5- Hmi5- |
0 |
4i3 |
0.00 |
0.89 |
|
AmiEmi, CG, FC |
-3c1-c2 |
i1+2i2+i3+i4 |
-2.33 |
3.06 |
Porovnání spojů
Dva harmonické spoje jsou ekvivalentní (podobné) jestliže všechny jednotlivé vazby jsou stejné (podobné). Např. [Dmi,Hmi5–] má tytéž vazby jako [Hmi5–,G]; [G,C] je ekvivalentní s [Emi,Ami].
Jiné faktory zanedbáváme.
Např. rozdíly skutečných (ne formálních) vazeb, nebo rozdíly způsobené
různou energií pásem,...
Dílčí spoje
Dílčí harmonický spoj zahrnuje nějakou podmnožinu vazeb harmonického spoje. Studium těchto podmnožin může být důležité pro rozlišení hudebních slohů.
Kvintové spojeUvedená tabulka kvintových spojů je tříděna podle hodnoty impulzu.
|
Spoj |
∑Spojitost |
∑Impulz |
øSpojitost |
øImpulz |
Kvinty |
|
cg-cg |
0 |
0 |
0.00 |
0.00 |
Identické |
|
cg-cf, cg-dg |
±2c1 |
i2 |
±3.00 |
1.63 |
Živé |
|
cg-a#d#, cg-ae |
±c2 |
i2+2i3 |
±0.75 |
2.63 |
Měkké |
|
cg-d#g#, cg-he |
±2c2 |
i1+i3 |
±1.50 |
3.50 |
Ostré |
|
cg-a#f, cg-da |
±c1 |
2i2+i3 |
±1.50 |
3.75 |
Měkké Mozartovy |
|
cg-c#g#, cg-hf# |
±c2 |
2i1 |
±0.75 |
6.00 |
Ostré Mozartovy |
|
cg-c#f# |
0 |
2i1 |
0.00 |
6.00 |
Neutrální |
Potenciál souzvuku
Javorskij Boleslav Leopoldovič| Javorskij Boleslav Leopoldovič [], 1877-1942, ruský hudební teoretik, tvůrce dynamické hudební koncepce, zásadně protikladné koncepci Riemannově. Odmítl pojetí hudební formy jako architektonické konstrukce, považoval ji především za jev procesuální, psychologický. Pracuje s utvářením a uvolňováním napětí, navrhl teorii stupnicového rytmu. Výrazně ovlivnil sovětskou muzikologii. |
Potenciál souzvuku je součtem potenciálů (F-potenciálů) všech zúčastněných pásem.
U(X) = ∑(U(Xi)/L, kde L je úroveň souzvuk, iε(0,L-1)
To je klíčový bod k pochopení funkční teorie harmonie předložené Riemannem. Každý tón souzvuku přispívá k celkovému potenciálu souzvuku. Každý tón je nositelem funkčnosti.
|
U(C) = U(Ami) |
6.33 |
|
U(Emi)= U(F) |
4.33 |
|
U(Dmi)= U(G) |
3.67 |
|
U( Hmi5-) |
1.33 |
Následující F-potenciály, U, odpovídají vybraným souzvukům přirozené modality:
Např. pro akord C:
U(C)=(c,e,g) =(Uc+ Ue+ Ug)/3= (6+6+7)/3
= 6.33
Formální potenciál (F-potenciál) souzvuku je dán součtem formálních potenciálů zůčastněných pásem.
Tóničnost souzvuk je formální potenciál snížený o entropii znění.
Kontrast potenciálů
Rozložení F-potentiálů v modalitě určuje jisté úrovně pro jednotlivé souzvuky. Rozdíl mezi potenciálovými hladinami vyúsťuje v napětí.
Kontrast potenciálů je definován:
F(i,j)= U(j) – U(i);
kde U(k) je potenciál souzvuk k.
|
i |
j |
i+j |
i∙j |
(i+j)/(i∙j) |
|
1 |
1 |
2 |
1 |
2.00 |
|
1 |
2 |
3 |
2 |
1.50 |
|
1 |
3 |
4 |
3 |
1.33 |
|
1 |
4 |
5 |
4 |
1.25 |
|
2 |
2 |
4 |
4 |
1.00 |
|
2 |
3 |
5 |
6 |
0.83 |
|
2 |
4 |
6 |
8 |
0.75 |
|
3 |
3 |
6 |
9 |
0.66 |
|
3 |
4 |
7 |
12 |
0.58 |
|
4 |
4 |
8 |
16 |
0.50 |
Energie vazeb závisí na energiích znějících tónů.
Když spoj má více vazeb, pak energie příslušející jedné vybrané vazbě je
nižší.
Tabulka zahrnuje poměr (i+j)/(i∙j) pro i, j <5.
Např. spoj dvou trojzvuků má 3+3 = 6 dílů energie a 3∙3= 9 vazeb.
Spoj dvou čtyřzvuků má 4+4 = 8 dílů energie a 4∙4= 16 vazeb.
Funkčnost
| Faktor | Spoj | Souzvuk |
| Spojitost |
Plynulost
g → c |
Konsonance
g c |
| Impulz |
Impulsivnost
h -- c |
Dizonance
c h |
|
Spojitost
+ impulz |
Funkčnost
g → c h -- c |
Entropie
c h g |
Spojitost činí zvuk daného spoje plynulým. Impulz přidává spoji výraz. Předpokládejme, že existuje taková charakteristika (působivost spoje), která závisí na obou zároveň.
|
Spoj |
Spojitost |
Impulz |
Součet |
|
Emi -F , |
1.67 |
4.89 |
4.78 |
|
Emi –Ami, G -C |
2.33 |
3.06 |
4.56 |
|
Hmi5-C , Ami-Hmi5- |
1.00 |
4.89 |
4.33 |
|
G -Ami, |
0.67 |
4.44 |
3.22 |
|
Hmi5-Emi, F -Hmi5- |
1.67 |
3.06 |
3.22 |
|
Emi -C , Ami-F |
2.00 |
1.89 |
2.89 |
|
Dmi –Emi, F -G |
0.00 |
4.44 |
2.78 |
|
C -Ami |
1.33 |
1.89 |
1.44 |
Spoje v tabulce jsou tříděné podle součtu spojitosti a impulzu.
Harmonická hustota
Hustota funkcí- počet harmonií v bloku, hustota změn polarity funkcí (popř. míra polarity funkce -T extrémní polarita)
- dominantní hustota maximální (8.0)- tónická hustota minimální (0.0)
Harmonické tendence
Každý tón má v kontextu modality jistou tendenci. Tato tendence závisí na struktuře modality, zvláště na potenciálu tónů a impulzu vazeb
Filip Miroslav| Filip Miroslav , 1932-1973, slovenský muzikolog a pedagog zabývající se hudební teorií a akustikou. V pojednání o vývoji klasické harmonie rozšířil pojem citlivého tónu o směrné tóny a směrné akordy. |
Impulzní tendence
Impulzní tendence jsoui analogické gravitační přitažlivosti.
Tóny spjaté vazbou impulzu nazveme vázané tóny. Protikladem vázaných tónů jsou volné tóny.
V následující tabulce jsou porovnány tři modality:
volné tóny vázané tóny
Přirozená pentatonika c,d,e,g,a ---
Přirozená diatonika d,g,a e,f,h,c
Úplná chromatika --- c,c#,d,...h
Diatoniky jsou nejvariabilnější modality, obsahují volné i vázané tóny.
Přirozená diatonika má vázané tóny e-f a h-c, viz tabulka.
| c d e f g a h | ∑(i)
--+-------------------------------------
c | 0 3 0 0 0 1 12 | 16
d | 3 0 3 1 0 0 1 | 8
e | 0 3 0 12 1 0 0 | 16
f | 0 1 12 0 3 0 0 | 16
g | 0 0 1 3 0 3 0 | 7
a | 1 0 0 0 3 0 3 | 7
h | 12 1 0 0 0 3 0 | 16
Impulsní spoj - natolik pevný, že sevře obě harmonie k sobě a oddělí je tak od sousedních v harmonickém proudu. Např. C-Hmi5–-Dmi-Ami ( před Dmi - nádech, "pomlka", prázdno ).
Hlavní a citlivé tóny
Uvažujme dva vázané tóny. Jestliže se potenciál těchto tónů liší,
pak tón s vyšším potenciálem nazveme hlavní tón a tón s nižším
potenciálem citlivý tón.
Např. v přirozené modalitě jsou hlavní tóny c,e, a citlivé tóny
h,f:
|
Tón |
c |
d |
e |
f |
g |
a |
h |
|
Impulz ∑(i) |
16 |
8 |
16 |
16 |
7 |
7 |
16 |
|
potenciál U |
6 |
4 |
6 |
0 |
7 |
7 |
0 |
Tón h má nízký potenciál a vazba h-c vysoký impulz. Přechod h-c má
za následek zánik tónu h. Po zániku tónu h, tón c vyniká (M.Filip).
Citlivé tóny bývají 'zaostřovány', tj. hrány blíže k hlavním tónům maximalizace impulzu). Tendence tóná vždy jistý směr. Rozlišujeme vzestupnou a sestupnou tendenci. Např. v přirozené modalitě, tón h má vzestupnou tendenci, zatímco tón f sestupnou tendenci.
Podle klasické teorie harmonie je tón c nejstabilnější. Tóny e, g jsou označovány také za stabilní, protože se váží na tón c. Tóny a,d,f jsou (v uvedeném pořadí) považovány za nestabilní a rozvádí se směrem dolů a=>g , dàc, f=>e. Nejlabilnější z tónů h se rozvádí směrem vzhůru hàc. Všechny chromatické tóny jsou nestabilní a mají tendenci k rozvedení do nejbližšího diatonického tónu. Předpokládá se ale, že je např. tón ab odlišný od tónu g#,
totiž rozvádí se ab=>g, g#=>a.
Modalitní struktura
Značky ß a =>znázorňují tendence tónů:
|
Přirozená |
Podhalská |
Harm. moll |
Cikánská |
|
|
Schéma |
221222(1) |
221212(2) |
212213(1) |
213113(1) |
|
Modalita |
cdefgahc |
cdef gg#a#c |
ahcdef g#a |
ahc d#ef g#a |
|
∑ |
5 4 5 3 5 5 3 5 |
6 3 2 4 4 2 3 6 |
5 2 4 2 6 3 2 5 |
3 3 4 3 6 3 4 3 |
|
Citlivé |
eß f ,h =>c |
e=> f , g ßg# |
h=> c , e ß f ,g# =>a |
d#=> e, e ßf,… |
Kvintová kostra
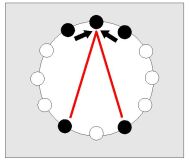 Kvintová kostra
sestává z minimálně dvou sousedících kvint, např. {f,c,g}.
Kvintová kostra
sestává z minimálně dvou sousedících kvint, např. {f,c,g}.
Kvintová kostra napomáhá nastolit kontrast v modalitách, zvláště v
případě půltónových jader.
Půltónové jádro je uskupení 2 půltonů vedle sebe, např. {h,c,c#}. Např. V
Bardosově modalitě {g,h,c,c#,f}, (struktura 1142(4)), má tón c velký
potenciál a tóny h,c# mají nejmenší potenciál.
|
Modalita |
Potenciály tónů |
Jádro |
|
Bardosova ( 327) |
h(-3) c(2) c#(-3) f(3) g(3) |
h(-3) c(2) c#(-3) |
|
Blues ( 663) |
g(4) g#(-5) a(2) c(8) d(4) f(3) |
g(4) g#(-5) a(2) |
|
Kombinovaná (1367) |
h(-2) c(2) c#(-2) d#(-1) f(4) g(4) h(-1) |
h(-2) c(2) c#(-2) |
Kvintová kostra podporující půltónové jádro je částí např. Bardosovy, blues, kombinované, cikánské a jiných modalit.
Tendence spojitosti
Tóny {h,f} mají nejnižší potenciál protože jejich vazby k ostatním tónům zahrnují jen jednu kvintu. Vypočítejme dva součty hodnot spojitosti.
| c d e f g a h | ∑c | ∑|c| ------------------------------------------------ c | 0 0 –2 +4 –4 0 0 | –2 | 10 d | 0 0 0 0 +4 –4 0 | 0 | 8 e | +2 0 0 0 0 +4 –4 | +2 | 10 f | –4 0 0 0 0 –2 0 | –6 | 6 g | +4 –4 0 0 0 0 –2 | –2 | 10 a | 0 +4 –4 +2 0 0 0 | +2 | 10 h | 0 0 +4 0 +2 0 0 | +6 | 6
První součet, ∑c, dává extrémní hodnotu pro tóny h (+6) a f(–6). Znaménka hodnot se liší - říkáme, že tón h má dominantní a tón f subdominantní tendenci.
Tóny s vyššími hodnotami součtu ∑|c| mají vyšší potenciál, tj.
vyšší stabilitu.
Tyto tóny jsou pilíři modality, vytváří hlavní kostru modality.
Citlivé tóny h,f vedou k tónům modalitní kostry c,e.
Čínské modality|
Základní mód |
Odvozené modality |
|
2232(3) |
22322(1); 22212(3); 222122(1) |
|
2323(2) |
23231(1); 23113(2); 231131(1) |
|
3232(2) |
32321(1); |
|
2322(3) |
23222(1); 23112(3); 231122(1) |
|
3223(2) |
32231(1); 32113(2); |
Zvláštním případem modalitních struktur založených na kvintové kostře a citlivých tónech jsou čínské modality. Vycházejí z pěti módů čínské pentatoniky, 2232(3). Půltóny byly přidány sdola ke kvintě a (nebo) oktávě.
Vliv barvy zvuku na melodii
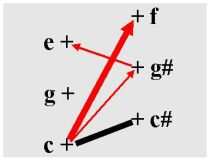 Spektrum alikvotních tónů ovlivňuje tendenci tónu.
Obvykle předpokládáme, že půltónový krok nemá
spojitost, jen impulz.
Spektrum alikvotních tónů ovlivňuje tendenci tónu.
Obvykle předpokládáme, že půltónový krok nemá
spojitost, jen impulz.
Nyní uvažujme hlavní alikvotní tóny.Vidíme silnou vazbu spojitosti
(c-f).
Například postupy půltónové ( h - c ) a celotónové ( d - c )
považujeme v
čisté podobě za obousměrné. Ve skutečnosti o jejich tendencích rozhodují jejich alikvoty.
Vazby vznikají mezi hf#d# - cge, resp.
df#a=>ceg.
Jediným intervalem, který zůstává barevnými spektry prakticky neovlivněn je
tritonus (viz např vazby mezi c#a#f# a egc.
Triton (symetrický interval) nemá ani spojitost, ani impulz; a není ovlivněn ani barvou zvuku.
Základní tón v kontextu
Tóny znějící před daným tónem nebo po něm mohou podporovat nebo rušit tendenci k základnosti.. Prof. Risinger ukazuje, jak hudební kontext může změnit základní tón (i konsonantnost) určitého souzvuku. Zvláštní pozornost přitom věnuje kvartě:
f 70% + 10% = 80%
c 30% - 10% = 20%
Uvažujme např. interval kvarty c-f, kde hlubší tón c bude zahrán velmi slabě - dostane jen 30% celkové energie (zatímco F 70% energie). Předpokládejme nyní, že vazba spojitosti c => f přesune 10% celkové energie a tedy způsobí, že c bude mít 20% a f 80% energie. Tehdy se f stává základním tónem a interval kvarty zní konsonantně.
f 30% + 10% = 40%
c 70% - 10% = 60%
V opačném případě, když c je silnější než g (což může nastat i například v dvojzvuku hraném tahem smyčce stejnou silou po obou strunách) dostaneme jiné rozložení energie. Interval kvarty zní disonantně (a vyšší tón vyžaduje rozvedení,...).
Změna modality
Modulace
Prokofjev Sergej Sergejevič| Prokofjev Sergej Sergejevič [], 1891-1953, ruský skladatel a klavírista, mistr vertikální polytonality, tj.zasouvání různých tónin do sebe. |
Modulace je změna stávající modality v modalitu jinou. V tomto smyslu je modulace velmi podobná harmonickému spoji.
Modulace je každá změna modality, příbuzné modality jsou takové, které mají obdobné rozložení formálních potenciálů. Působení modulace závisí především na impulzu. Největšího impulzu se dosahuje zpravidla posunem celé modality o půltón.
Rozlišujeme dva základní druhy modulace:
Translace modality, tj. změna modality při zachování struktury.
Deformace modality, tj. změna modalitní struktury
Beze změny tóniky
Se změnou tóniky
Účinek modulace závisí na trvání přechodu k nové modalitě. Souzvuk tónů, které jsou oběma modalitám společné, představuje jakýsi teoretický přechod mezi modalitami. Ale ne pro všechny modulace existuje takový (vhodný) souzvuk (tóniny).
Představme si uskupení modality promítnuté do souřadné soustavy. Svislá osa nechť reprezentuje potenciál uskupení a vodorovná osa spojitost k tónice. Každý souzvuk a i každá modalita tak získá své souřadnice. Počátkem soustavy je tónika.
Podobnost modalit
Podobnost modalit je dána charakteristikami jejich vzájemných
vazeb.
Závisí na počtu společných tónů, spojitosti, impulzu, potenciálech tónů.
Např. porovnejme dva páry modalit:
1/ [cdefgab]-[c#defg#ab] a 2/ [cdefgab]-[cd#ef#gab]
Modality mají dva odlišné tóny 1/ {c-c#, g-g#}, 2/{d-d#,f-f#}.
V případě 1/ se mění základní tónické tóny {c,g};
modality jsou proto méně podobné.
Nechť v(A,B) je součtem hodnot (např. spojitosti, impulzu,...) pro všechny vazby z modality A do modality B. Pak podobnost r(A,B) modalit A a B je:
r(A,B) = |v(A,B) – v(B,A)|
Oscilace
Oscilace modality je opakující se deformace modality.
Často se oscilace dotýká jen několika vybraných tónů. Ostatní tóny zůstavají pevné. (Pevné tóny tvoří kostru pro všechny modality. Mohly by tedy mít vysoký potenciál v kterékoliv z modalit).
Mozart Wolfgang Amadeus| Mozart Wolfgang Amadeus [mócárt], 1756-1791, rakouský skladatel, jeden z největších hudebních géniů všech dob. |
V následující ukázce z Mozartovy opery Don Giovanni se modalita mění s každým akordem.
|
Harmony |
Modality |
Scheme |
p |
|
X: |
a,h,c,d,e,f#,g# |
#10#111 |
4 |
|
Ami: |
a,h,c,d,e,f,g |
#10#100 |
2 |
|
Dmi6-: |
a,a#,c,d,eb,f,g |
#00#011 |
2 |
|
G, Ami: |
a,h,c,d,e,f,g |
#10#100 |
2 |
|
A: |
a,h,c#,d,e,f,g |
#11#100 |
3 |
|
Dmi: |
a,h,c#,d,e,f,g |
#11#100 |
3 |
|
a,a#,c,d,e,f,g |
#00#100 |
1 |
|
|
A#, F7: |
a,a#,c,d,eb,f,g |
#00#000 |
0 |
|
Ami,Esus4,E: |
a,h,c,d,e,f#,g# |
#10#111 |
4 |
|
Ami |
... |
Pevnými tóny jsou zde {a,d} (označeny #), ostatní tóny oscilují (označeny 0,1), p-počet jedniček.
Schéma oscilace: (a),(a#,h),(c,c#),(d),(eb,e),(f,f#),(g,g#)
Oscilace modality mění rozložení potenciálů. Tím vznikají nové
tendence tónů, mění se citlivé tóny, harmonické funkce,...
Např. vzestupná melodická moll stupnice tvoří modalitu {a,h,c,d,e,f#,g#}
s durovou dominantou i subdominantou, D={e,g#,h}, S = {d,f#,a}.
Tatáž stupnice sestupná tvoří přirozenou modalitu {a,h,c,d,e,f,g} s molovými dominantami S={d,f,a}, D={e,g,h}.
Neurčitost modality
Při analyze skladby je nutné v každém okamžiku určit stávající modalitu a vznikající relace posuzovat v jejím kontextu. modalitu přitom určují jen a pouze ta pásma, která získávají energii od tónů.
Úvahy o pevně daných modalitách a uskupeních tónů jsou však
idealizace. Ve skutečnosti existuje předivo hlasů, které tyto útvary
tvoří dynamicky.
Mimotonální tóny bývají tolerovány zejména tehdy, pokud jejich energie
záhy zaniknou v důsledku reaktivnosti pásem. Tak je tomu právě v případě
neapolského sextakordu; energie v pásmech c#,g# jsou zrušeny nástupem
tónů dominanty d,g.
Přesné vymezení modality se utváří až postupným vyzníváním jednotlivých tónů, sestavováním celku z dílčích skladebných struktur.
Mozart - Turecký pochod - v několika prvních taktech se objeví 10
tónů(všechny kromě f# a c#), ne všechny ale mají stejnou váhu.
Změna
podstruktur základní modality je spjata s průběhem zúčastněných
melodických linií. Nejužší vazba je ve skladbách jednohlasých, proto jsou
tyto ( lidové písně a pod. ) nejvhodnějším materiálem pro výzkum
melodických tendencí.
=> melodické tendence. Např. nechť fráze s tóny {c,d,e,f,g,a,h} je
rozdělena do dvou samostatných částí s tóny {c,e,f,g,a} a
{f,a,h,c,d}.
Nezávislá kombinace dvou modalit není totéž jako sjednocení.
Tam kde známe jen jeden hlas (např. nápěv lidové písně) je zařazení
obtížné.
Např. nápěv {c,d,e,f,g} nemusí patřit modalitě {c,d,e,f,g}. Mohl být
zpíván dvojhlasně zároveň s {a,h,c,d,e}; pak by patřil modalitě
{a,h,c,d,e,f,g}.
Nebo mohl být hrán s akordickým doprovodem, např. C,C#,Fmi. Tomu by
odpovídala modalita {c,c#,d,e,f,g,g#}.
Možná harmonizace shora (např. pentatoniku lze harmonizovat diatonicky, nikoliv tritonicky) ((((tritonika) pentatonika) diatonika) chromatika)
Závěr fráze
Přesvědčivost závěru je mírou uvolnění. Spoj činí přesvědčivý závěr jestliže respektuje toto schema.
extrémní
malý ════════► velký
potenciál spojitost potenciál
Klamný závěr
Klamný závěr je spoj vedoucí do akordu, který má extrémní
potenciál, ale ne s extrémní spojitostí; např. G-Ami.
Posluchač slyší stabilní souzvuk, ale tento souzvuk se objevuje takovým
způsobem, že jej nemůže přijmout jako definitivní konec.
Návraty k T na koncích veršů, když verš opakován, první závěr klamným spojem:
C,G7,C,C7 - Kde domov můj, kde domov můj, voda
F,C,F,C - hučí po lučinách, bory šumí po skalinách
G7,C,G7,C - v sadě skví se jara květ, zemský ráj to na pohled
E,Ami - a to je ta krásná země
F,C,G7,Ami - země česká, domov můj
F#dim,C,G7,C - země česká domov můj
Harmonické sekvence
Barokní sekvence
|
Harmonický spoj |
Spojitost |
Impulz |
|
EmiAmi, GC, CF |
+2.33 |
3.06 |
|
Hmi5-Emi, Fhmi5- |
+1.67 |
3.06 |
|
DmiG |
+1.33 |
2.61 |
V barokní hudbě najdeme často sled
C:F:Hmi5-:Emi:Ami:Dmi:G:C. V barokní hudbě se často objevuje
sled C:F:Hmi5-:Emi:Ami:Dmi:G:C, [2]. Ve všech
dílčích spojích najdeme vysoké hodnoty spojitosti (1.56, 1.11, 0.89) mezi
konsonantními trojzvuky přirozené modality.
Průměrná spojitost sekvence je rovna průměru spojitostí jednotlivých spojů:
c(s) = [c(C,F) +c(F,Hmi5-) +c(Hmi5-,Emi)
+c(Emi,Ami) +c(Ami,Dmi) +c(Dmi,G) +c(G,C)]/7
c(s) = (2.33+1.67+1.67+2.33+2.33+1.33+2.33)/ = +14/7= 2.00
Z Mozartovy hudby
V úvodu Mozartovy předehry k opeře Don Giovanni zní:

Spojitost (červené šipky) je soustředěna spíše do nižších poloh hlasů
(fagot,violy,nižší houslové polohy). V hlasech fagotu a houslí jsou
patrné nástupy spojitosti s čtytaktovou periodou. Postupy v impulzních
intervalech (černé šipky) jsou svěřeny především partům druhých
houslí.
Jazzové sekvence
Jazzové sekvence [11] jsou sekvence s převahou hodnoty impulzu, to platí zejména o chromatické jazzové sekvenci (např. E7:D7:C7:H7)
Normální jazzová sekvence (např. Ami7:D7:Gmi7:C7) se průběhem spojitosti blíží sekvenci barokní.
Vivaldi - melodie - vedoucí hlas (nejživější) nastupuje až na lehkou dobu ( na těžkou dobu doprovodné hlasy - polyfonie - komplementární
- rozsah - až 2-oktávový ( rozložený akord ); - tirata - přetahování tónů přes taktovou čáru ( zajistí se sjednocení -totožnost na vazbách mezi takty )
- Bach - harmonie- přirozená dur;harmonická moll; méně časté spoje: II-S,S-III, D-II, D-III, VI-T,VII-S,VII-VI; X-D(X)
- motivy - kratičké, v sekvencích ( max 3,4 souzvuky) o 7,5 i tercii; o
sekundu velmi řídce; - melodie - všechny tři mollové rovnocenně, zpravidla melodická vzhůru, přirozená(aiolská) dolů - figury melodické prosté - Mozart
- vyrovnání entropie akordů v harm. proudu - melodie krouží kolem akordických tónů (atraktory...) co nejblíže (v půltón krocích,..)
- Beethoven - tóny s nízkým form. potenciálem v base
- figury melodické v kombinaci s harmonickými
Soustavy - čínské - harmonie T,D; začátek T, konec D ; nezná modulaci - akordy - max.cfc nebo cgc (kvintové a kvartové paralelismy); (ne dur,moll..); v závěru jako souzvuk sekunda; - motivy - zpravidla dva v poměru 7 (gfd-cbg); - melodie - nikdy nekončí T přes 7. stupeň; m.3 - mel.krok, v.3 -skok (tzn. neex. podvojnost 3); v.3 - intonačně labilní, zvyšována až o čtvrttón.; - rozsah - [>12] neobvyklé skoky ( vysoká poloha 1,2)
Neobvyklé spoje
Každý hudební sloh má pevné hranice pro hodnoty jistých charakteristik. Spoje, které z těchto hranic vybočují jsou považovány za neobvyklé nebo jsou přímo slohovými pravidly zakázány. Omezením přitom nemusí podléhat jen celý harmonický spoj, ale i každá jeho podmnožina; např. zákaz paralelních kvint a oktáv v klasické harmonii. Některá z pravidel nutí zase dílčí jevy podřizovat se zákonům celku. Např. pravidla pro přísné vedení hlasů v klasické harmonii dovolují jen takový pohyb hlasů, kdy celková změna výšek všech hlasů je minimální.
Přípustné spoje
Každý harmonický spoj je přípustný. Ale každý spoj je vnímán ve
vztahu k hudební soustavě, modalitě, tónině,...
Ne všechny kombinace napětí jsou přirozené a zní dobře.
Např. různá pravidla připouští nebo zakazují některé druhy kvint v
harmonických spojích.
Janáček psal o nesprávnosti cg-a#f. Jiní teoretikové označují za (v
některých kontextech) nesprávný inverzní spoj cg-da (měkké Mozartovy
kvinty).
Přísný spoj
Klasický přísný harmonický spoj musí vyhovovat následujícím pravidlům:
Postup o sekundu - Všechny horní hlasy by měly vést k nejbližším tónům (v protipohybu s basem).
Postup o kvartu nebo kvintu -Každý z horních hlasů by měl postupovat nejvýše o tercii (bez změny hlasů)
Postup o tercii - Každý z horních hlasů by měl postupovat nejvýše o kvartu (v protipohybu s basem).
Tato pravidla byla a jsou respektována také v jiných stylech, převážně ve středních hlasech polyfonie.
Neobvyklé spoje klasické hudby
Přirozená modalitaSouzvuky s nejvyšší spojitostí k tónice (dominanty) byly jen zřídka spojovány s jinými než tónickými tóny. Spoje vycházející z dominanty tříděné podle hodnoty spojitosti:
|
Spoj |
Spojitost |
Impulz |
Poznámka |
Spojitost |
Impulz |
Rozdíl |
|
GC |
3c1+c2 |
i1+2i2+i3+i4 |
k tónice |
+2.33 |
3.06 |
-0.73 |
|
GEmi |
2c1 |
i2+2i3 |
+1.33 |
1.89 |
-0.56 |
|
|
GAmi |
c1 |
i1+4i2+i3 |
klamný spoj |
+0.67 |
4.44 |
-3.77 |
|
GF |
i1+4i2+i3 |
neobvyklý |
0.00 |
4.44 |
-4.44 |
|
|
GHmi5- |
-c1-c2 |
i2+3i3+i4 |
komplex G7 |
-1.00 |
1.44 |
-2.44 |
|
GDmi |
-2c1 |
3i2+2i3 |
neobvyklý |
-1.33 |
2.61 |
-3.94 |
Spoje vycházející z dominanty tříděné podle hodnoty spojitosti:
|
Spoj |
Spojitost |
Impulz |
Poznámka |
Spojitost |
Impulz |
Rozdíl |
|
EAmi |
2c1+c2 |
2i1+i2+3i4 |
k tónice |
+1.67 |
3.56 |
-1.89 |
|
EF |
c1 |
3i1+i2+i3+2i4 |
+0.67 |
5.06 |
-4.39 |
|
|
EDmi |
c1 |
2i1+2i2+2i3 |
neobvyklý |
+0.67 |
4.56 |
-3.89 |
|
EC5+ |
c1 |
i1 |
+0.67 |
1.33 |
-0.67 |
|
|
EHmi5- |
-c1 |
i1+i2+3i3 |
neobvyklý |
-0.67 |
2.72 |
-3.39 |
|
EG#5- |
-c1-c2 |
i2+3i3+i4 |
komplex E7 |
-1.00 |
1.44 |
-2.44 |
Jiné neobvyklé spoje: AmiC,DmiF,EmiG (přirozená modalita), FAmi, Hmi5-Dmi (harmonická moll modalita)
|
Harmonický spoj |
Poznámka |
Spojitost |
Impulz |
|
Hmi5-Dmi |
komplex Hmi7/5- |
-1.00 |
1.44 |
|
AmiC (DmiF, EmiG) |
komplex Ami7 |
-1.33 |
1.89 |
|
FAmi (CEmi) |
komplex Fmaj7 |
-2.00 |
1.89 |
Harmonická kostra melodie
 Harmonická
kostra
Harmonická
kostra
Harmonická síla je celková (časově integrovaná) energie v pásmech.
Harmonická kostra melodie je množina tónů, které přispívají nejvíce k
harmonické síle.
Akordickým tónem je každý tón daného akordu. Jestliže se objeví jiný tón,
zatímco daný akord stále zní, nazýváme takový tón neakordický.
Harmonická kostra melodie obvykle sestává z akordických tónů. Stabilita
melodie závisí na počtu a umístění (lehké x těžké doby) neakordických
tónů.
Např. mějme dva akordy {F,G}. Melodie {a,h,d,c} má poněkud jinou
stabilitu než melodie {h,a,c,d}. V první jsou akordické tóny {a,d} na
těžkých dobách, ve druhé na dobách lehkých.
Harmonické krytí
Harmonické krytí je mírou harmonické stability melodie.
Definujeme: c = a/d,
kde d je délka dané fráze (obvykle trvání souzvuku), a je trvání
akordických tónů.
Např.:
|
Harmonie |
Melodie g,h,c,f |
Harmonické krytí |
|
|
Dmi |
x x x 1 |
1/4 = 0.25 |
|
|
Ami |
x x 1 x |
||
|
C |
1 x 1 x |
2/4 = 0.50 |
|
|
Hmi- |
x 1 x 1 |
||
|
Emi(G) |
1 1 x x |
||
|
F |
x x 1 1 |
||
|
C-F |
1 x 1 1 |
3/4 = 0.75 |
|
|
G-C |
1 1 1 x |
||
|
G-F |
1 1 1 1 |
4/4 = 1.00 |
Každá hudební fráze má jisté meze hodnot harmonického krytí. Nižší
harmonické krytí je obvykle dovoleno jen v případě větší pohyblivosti
melodie.
Např. rozložené akordy mají c=1.00, melodické ozdoby přibližně c=0.5.
Melodie s c<0.5 se objevují jen zřídka (např. blue tóny).
Blue tóny
Blue tóny jsou zvláštním případem neakordických tónů. Melodie užívá jinou
modalitu než harmonie.
Např. zatímco souzvuky respektují přirozenou modalitu, nápěv užívá tónů
blues modality.
Blue tóny jsou často půl tónu pod akordickými tóny.
|
Akord |
Äkordické tóny |
Blue tóny |
|
C7 |
c,e,g,b |
d#,f#,a#,(g#) |
|
Dmi7 |
d,f,a,c |
g#,(a#) |
|
G7 |
g,b,d,f |
a# |
|
Ami |
a,c,e |
d#,(f),(g) |