Schematická algebra - Speciální případy
Případy R-systémů
V předchozí kapitole jsme se zabývali obecnými úvahami o R-systémech, prošli jsme:
prosté R-systémy (r ε P) a složené R-systémy (obecný případ r)V této a některých dalších kapitolách soustředíme pozornost na některé specielní případy.
V této kapitole:
G-systémy (r=nk−1) binární G-systémy (r=nk−1, n=2) M-systémy (r = (nk−1)/(n−1)) F-systémy (r = nh+1) K-systémy (r = (nk+1)/(n+1))--------
systémy komplexních čísel (u ε K) systémy algebraických čísel (u ε A) znaménkové S-systémyV dalších kapitolách:
systémy mocninných zbytků (k=κ(r,v)) systémy primitivních kořenů (k=r−1) Legendreovy systémy (k=κ(r,v) kde u=v pro u z prvního řádku) nasycené systémy (n=k) - Wieferichovy systémy (r=t²)G-systémy
Oblast, kterou zde studujeme, je v kombinační teorii známa jako Kombinatorika náhrdelníků (Combinatorics of necklaces).
Instance
Uvažujme uspořádání n prvků do k buněk. Nechť A je množina s n členy (prvky) a E(A) = {0, 1, .., n−1} množina ordinálních čísel těchto členů. Nechť dále B je množina s k členy (buňkami) a ξ relace z E(B) do E(A).
000 001 010 100 011 110 101 111
ξ
(buňky) E(B) ─────────────> E(A) (prvky)
Zavedeme-li čísla E(B) jako pozice čísel (číslic) z E(A), získáme přepisem do n-kové soustavy nk čísel. Množinu všech těchto čísel označme I(n,k), prvky této množiny jsou tzv. instance. Číslo n nazveme základem a k řádem množiny instancí.
Např. množinám A={p, q}, B={x, y, z} odpovídají množiny ordinálních čísel E(A)={0, 1}, E(B)={0, 1, 2}.
Boole George| Boole George , [búl] 1815-1864, irský matematik, tvůrce první algebry matematické logiky. Zabýval se také kvaterniony a teorií pravděpodobnosti. Jeho jméno dostal používaný systém logiky a -v počítačové terminologii- také typ proměnných, které nabývají právě dvou hodnot (pravda, nepravda). |
Výsledné pravdivostní hodnoty funkcí logického součtu (or) i součinu (and) je možné rozčlenit podle zadaných hodnot (A=ano,N=ne):
Dané hodnoty and or
────────────────────────
NNN N N
NNA NAN ANN N A
NAA AAN ANA N A
AAA A A
Uvažujme množinu M sestávající ze 3 prvků {A,B,C}.
Krychle
000 {}
001 010 100 {A} {B} {C}
011 110 101 {A,B} {B,C} {A,C}
111 {A,B,C}
Instance systému G(2,3) vytvářejí podmnožiny dané množiny M.
Instance G(2,k) představují souřadnice vrcholů k-rozměrné krychle, pro k=3 trojrozměrné krychle. Každá instance G(2,3) odpovídá jednomu vrcholu, úroveň instance udává vzdálenost od počátku.
V krystalografii se používá k určení rovin tzv. Millerových indexů (h,k,l). Indexy udávají vzdálenosti průsečíků dané roviny (nebo některé s ní rovnoběžné) se souřadnými osami od počátku souřadnic. Čárka zapsaná nad indexem značí, že rovina protíná osu v záporných hodnotách.
Spojením středů stěn krychle vzniká osmistěn.

Tento osmistěn je určen Millerovými indexy se strukturou G(2,3).
V geometrické představě jsou instance rozlišeny jen podle úrovní, nikoliv podle druhů.
Druhy instancí
Budiž relace G, definována následovně, nazývána G-relace.
ui (j) = nj ∙ gi (mod r), r = nk−1
Relace G je relací ekvivalence, rozloží tedy instance ui (j) na druhy I(n,k)/G.
Protože modul r = nk−1, je celkový počet instancí r+1 = nk, kde n je základ a k řád G-systému. Každý druh má jednoho svého zástupce (reprezentanta), reprezentanty druhů značíme gi.
Instancí daného druhu se nazývajítranspozice. Množinu instancí s
G-relací nazýváme G-systém a značíme G(n,k). Každý G(n,k) má m(n,k) druhů
označených gi, i=1..m.
Systém G(2,3) má 2³=8 instancí I(2,3)={000, 001,.., 111}
členěných do m=4 druhů.
V případě 12-ti tónové soustavy je n=2, k=12 a
struktury utváří G(2,12). Když A={existuje, neexistuje} a B={c, c#, d,
d#, e, f, f#, g, g#, a, a#, h},
utvářejí množiny ordinálních čísel E(A)={0,1}, E(B)={0, 1, .., 11}
a relace ξ množinu I(2,12).
Zmenšený septimový akord (c,d#,f#,a) je druh z I(2,12) se
3-mi transpozicemi:
0/ 001001001001 [c, d#, f#, a]
1/ 010010010010 [c#, e, g, a#]
2/ 100100100100 [d, f, g#, h]
Jednotlivé instance G-systému vznikají variacemi k-té třídy z n
prvků a je jich celkem nk. Mezi instancemi jsou vždy všechny
možné permutace s opakováním vybraných prvků.
V G(3,5) je 30 různých instancí se dvěma nulami, dvěma jedničkami a
jednou dvojkou, tj. 00112, 01120, 11200, 12001,... Příslušných permutací
s opakováním je 5!/(2!2!1!) = 30, k=5 zaplní instance právě 30/5 = 6
druhů.
V binárních systémech, tj. v systémech kde n=2 je počet permutací s opakováním roven počtu kombinací. Např. v G(2,5):
1∙
00000
5!/5!0! = 1 =
![]()
5∙
00001
5!/4!1! = 5 =
![]()
5∙ 00011 + 5∙ 00101 5!/3!2!
=10 =
![]()
5∙ 00111 + 5∙ 01011 5!/2!3!
=10 =
![]()
5∙
01111
5!/1!4! = 5 =
![]()
1∙
11111
5!/0!5! = 1 =
![]()
Typy schemat
Rozlišíme tři typy schemat: základní, kontrastní a symetrické schema:
Základní schema Kontrastní schema Symetrické schema ────────────── ──────────────── ───────────────── 0 15 0 1 2 4 8 14 13 11 7 1 2 4 −7 3 6 12 9 12 9 3 6 3 6 −3 −6 5 10 10 5 5 −5 7 14 13 11 8 1 2 4 7 −1 −2 −4 15 0 0
V některých případech je některé schema vhodnější, typ použitých schemat budeme proto dále podle okolností střídat.
DeformacePro r=15 je obor Z15 průmětem (homomorfizmem) oboru Z.
Celá čísla Množina instancí a druhů
────────────────────────────────────────
0 0
1 2 4 8 1
Z ────> 3 6 12 9 ────> 3
5 10 5
7 14 13 11 7
15 15
Prvky oboru Z15 tvoří např. instance G-systému G(2,4,15).
Na čísla druhů v G(2,4,15) můžeme nahlížet jako na deformaci (morfizmus) čísel instancí.
Kdyby mělo být zobrazení z množiny instancí na množinu druhů průmětem, musela by existovat operace mezi čísly druhů odpovídající operaci mezi čísly instancí.
Úroveň druhu
Součet čísel (číslic) označujících jednotlivé prvky libovolné instance daného druhu g v G(n,k) nazveme úroveň L(g).
Např. v systémech G(2,k) určuje úroveň druhu počet jedniček v libovolné jeho instanci.
V našem příkladě G(2,4) mají druhy následující úrovně:
i/ Druh gi Binární schemata Úroveň L(gi) ──────────────────────────────────────────────── 1/ 0 0000 0 2/ 1 0001 0010 0100 1000 1 3/ 3 0011 0110 1100 1001 2 4/ 5 0101 1010 2 5/ 7 0111 1110 1101 1011 3 6/ 15 1111 4
Generování schémat instancí
Algoritmus pro výpis čísel reprezentantů druhů G-systému je podobný Eratosthenovu sítu (viz Dělitelnost čísel). V našem případě potřebujeme vyčlenit čísla reprezentantů druhů z čísel všech instancí. Analogií prvočíselných násobků jsou v G-systémech transpozice instancí.
Např. v G(2,4) je základ n=2, řád k=4 a modul r = nk−1 =
24−1=15.
Budeme škrtat čísla g∙nj (mod r), j=1,2,..., kde za g vezmeme
vždy nejmenší nepoužité číslo.
Čísla, která budeme škrtat, nás zajímají - zapisujeme je do schémat (vpravo). Na rozdíl od Eratosthenova síta vyškrtáme postupně vše.
Daná čísla: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
Použitá čísla Vybraná (vyškrtaná) čísla
I/ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 0
II/ 3,5,6,7,9,10,11,12,13,14,15 1 2 4 8
III/ 5,7,10,11,13,14,15 3 6 12 9
IV/ 7,11,13,14,15 5 10
V/ 15 7 14 13 11
15
Algoritmus
Označme množinu všech vyškrtnutých čísel X. Následující vývojový diagram popisuje algoritmus generování schémat instancí G-systému:
vyprázdni množinu X
↓
+--+- pro g=0 to (n(k-1)-1) -- zapiš poslední druh g=nk-1
| | |
| ↑ is class g in X ?
| | |
| +- YES-----+
| |NO
| |
| zapiš g to X
| ↓
| přiřaď u <- g
| |
|+---> dokud není u v X ----+
|| | |
|| zapiš u to X |
|| | |
|| transponuj instanci |
|| u <- n * u |
|+------<-----+ |
+-------------<-------------+
Uvedený algoritmus se ale může ukázat pro rozměrnější systémy nevýhodný.
Např. jen k vytvoření všech druhů systému G(2,24) potřebujeme k evidenci všech zaškrtnutých čísel 2 MB (megabajty) paměťového prostoru: 1 zašktrtnutí=1 bit, 1 bajt = 2³ bitů, 1 megabajt=220 bajtů.
Definujme g-číslo druhu jako minimum ze všech čísel instancí (všech transpozic) daného druhu:
g = min(u0,u1,u2,..,uk−1) = min(u, u∙n mod r, u∙n² mod r,...u∙nk−1 mod r)
Tedy pro libovolné číslo u můžeme určit číslo g - odtud algoritmus:
│
┌───> pro u=0 to (nk−1−1) ──> zapiš
poslední druh g=nk−1
│
│
│ urči g <− min(u,u∙n mod r,...)
│
│
│ is g = u ──> vypiš instance druhu g
│
│
└──────<──────┴──────<──────┼
Druhý algoritmus je časově náročnější. Ke zrychlení je nutné hledat heuristiky, např. v případě binárních systémů nemůže být g−číslo druhu sudé....
Příklady výstupu
G(n,1)
G(2,1) G(3,1) G(4,1)
0 0 0
1 1 1
2 2
3
G(2,2) G(3,2) G(4,2)
0 0 0 6 9
1 2 1 3 1 4 7 13
3 2 6 2 8 10
4 3 12 11 14
5 7 5 15
8
G(2,3) G(3,3) G(4,3)
0 0 0 21
1 2 4 1 3 9 1 4 16 22 25 37
3 6 5 2 6 18 2 8 32 23 29 53
7 4 12 10 3 12 48 26 41 38
5 15 19 5 20 17 27 45 54
7 21 11 6 24 33 30 57 39
8 24 20 7 28 49 31 61 55
13 9 36 18 42
14 16 22 10 40 34 43 46 58
17 25 23 11 44 50 47 62 59
26 13 52 19 63
14 56 35
15 60 51
Program pro výpis druhů
Náznak programu pro G-systém G(n,k) (n=this.Degree, k=this.Order):
var r = (decimal)Math.Pow(this.Degree, this.Order) - 1;
this.Marked = new BitArray(r + 1, false);
var g = 1;
while (g ≤ r) {
if (g < this.Marked.Count && !this.Marked.Get(g)) {
this.AddStructure(g);
this.MarkInstancesOfClass(g, r, marked);
}
g = g + 1;
}
void MarkInstancesOfClass(int g, int r) {
var u = g;
while (u ≥ 0 && u < r && u < this.Marked.Count && !his.Marked.Get(u)) {
if (u < this.Marked.Count) {
this.Marked.Set(u, true);
}
u *= this.Degree;
while (u > r) {
u -= r;
}
}
}
Náznak programu pro binární G-systém G(n,k) (n=this.Degree=2, k=this.Order):
var r = (decimal)Math.Pow(this.Degree, this.Order - 1) - 1;
long num;
for (num = 1; num ≤ r; num += 2) {
decimal classNumber = this.DetermineClassNumber(this.Order, num);
if (num == classNumber) {
this.AddStructure(num);
}
}
num = (long)Math.Pow(this.GSystem.Degree, this.GSystem.Order) - 1;
this.AddStructure(num);
long DetermineClassNumber(byte order, long number) {
var minNum = number;
for (byte n = 1; n < order; n++) {
number = this.TransposeLeft(order, number);
if (number < minNum) {
minNum = number;
}
}
return minNum;
}
long TransposeLeft(int order, long number) {
var shift = (byte)(order - 1);
return (number & 1) << shift | number >> 1;
}
Pravidla dělitelnosti
Číslo instance ui (j) je soudělné s r=(nk−1), právě když odpovídající číslo druhu gi je soudělné s r. Počet všech čísel, která nejsou soudělná s r je φ(r), kde φ je Eulerova funkce.
Jestliže gi není soudělné s r, pak jeho druh musí být vlastní (ne vnořený) a takový druh má k instancí. Proto k | φ(nk−1), tj.:
φ(nk−1) mod k = 0
G(2,4)
0
* 1 2 4 8
3 6 12 9
5 10
* 7 14 13 11
15
V G(2,4) jsou nesoudělné s 24 −1=15 instance: (1, 2, 4, 8) a (7, 14, 13, 11), tj.řádky označené hvězdičkou. Protože φ(24−1)=φ(15)=8 je φ(nk−1) mod k=8 mod 4=0.
Druhy g, pro které (g,r)=1, nazveme Eulerovy druhy, zkráceně E-druhy. Zahrnují celkem E=φ(r) instancí členěných do e=E/k = φ(r)/k druhů.
Koeficient g(n,k) = φ(nk−1)/k
n \ k │ 1 2 3 4 5 6 7 8 9 10
──────┼─────────────────────────────────────────────────
1 │ − − − − − − − − − −
2 │ 1 1 2 2 6 6 18 16 48 60
3 │ 1 2 4 8 22 48 156 320 1008
4 │ 1 4 12 32 120 288 1512 4096
5 │ 2 4 20 48 280 720 5580
6 │ 4 12 56 216 1240
7 │ 2 8 36 160
8 │ 6 18 144
9 │ 4 16 96
10 │ 6 30
n \ k │ 11 12 13 14 15 16 17 18 19
──────┼────────────────────────────────────────────┼
2 │ 176 144 630 756 1800 2048 7710 7776 27594
Domněnka: pro sudá k (n>2), k | g(n,k).
Když seřadíme binární čísla instancí G(2,4) za sebe tak, aby se sousední dvě lišily vždy jen jedním prvkem [Vrba] dostaneme:
Binární čísla Dekadický zápis
─────────────────────────────────────────────────────────────────
0000,0001,0011,0010,0110,0111,0101,0100 0, 1, 3, 2, 6, 7,5,4
1100,1101,1111,1110,1010,1011,1001,1000; 12,13,15,14,10,11,9,8
Na lichých pozicích jsou čísla nesoudělná s modulem 15:
Liché pozice:1,2,7,4,13,14,11,8
Sudé pozice:0,3,6,5,12,15,10,9
G-systémy jsou postaveny nad relací G, kterou tvoří kongruence podle modulu nk−1., kde n je základ a k řád G-systému. Relace G je ekvivalence na množině všech instancí U. Třída ekvivalence G je množina všech instancí daného druhu.
Faktorová množina U/G je množina všech druhů (tříd ekvivalence), tj. rozklad množiny U na jednotlivé množiny instancí podle druhů. Každá instance u ε U, patří právě k jednomu druhu g(u). Zařazení instance k některému druhu pG: G−> U/G se nazývá projekce.
M-systémy
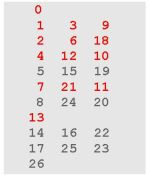 Předpokládejme systémy R(n,k,r), kde:
Předpokládejme systémy R(n,k,r), kde:
r = (nk−1)/(n−1)
Tyto systémy budeme nazývat Mersennovy (M-) systémy a značit
M(n,k). Systém M(n,k) má r+1 instancí {0,..,r}.
Při n=2 M-systémy splývají s G-systémy, neboť dělitel (n−1)=1. Systémy M(2,k) tedy mají r+1 = (2k−1)/(2−1)+1 = 2k instancí.
Algoritmus pro M-systémy
Algoritmus generování M-systémů se od algoritmu pro G-systémy (viz Algoritmus pro G-systémy) neliší v ničem jiném, než v hodnotě r.
Příklady výstupu
M(2,1) M(3,1) M(4,1)
0 0 0
1 1 1
M(2,2) M(3,2) M(4,2)
0 0 0
1 2 1 3 1 4
3 2 2 3
4 5
M(2,3) M(3,3) M(4,3)
0 0 0
1 2 4 1 3 9 1 4 16
3 6 5 2 6 5 2 8 11
7 4 12 10 3 12 6
7 8 11 5 20 17
13 7
9 15 18
10 19 13
14
21
Když kεP má M-systém (nk−n)/(n−1) vlastních druhů a tedy k | (nk−n)/(n−1) − protože je v tomto případě (n−1,k)=1, nedozvídáme se nic více, než říká Malá Fermatova věta (viz)
Čísla nesoudělná s r jsou vždy podmnožinou vlastních instancí, odpovídající druhy mají tedy vždy k transpozic a platí: k | φ(r) tj. k | φ((nk−1)/(n−1))
Z vlastnosti G-systémů k\φ(nk−1) a z malé Fermatovy věty k\(nk−n) pro kεP, (k,n)= 1 plyne:
(nk−n)−φ(nk−1)≡0 (mod k) tj. (nk−1+1−n)−φ(nk−1)≡0 (mod k)
Výraz nk−1−φ(nk−1) můžeme nahradit ψ(nk−1) (viz Eulerova funkce). Platí tedy:
Ψ(nk−1) ≡ n−1 (mod k)
Počet čísel soudělných s nk−1 patří do stejné zbytkové třídy (mod k) jako n−1. Např.:
ψ(5³−1) ≡ 124 ≡ 1 (mod 3) (5−1)≡ 1 (mod 3)
ψ(27−1) ≡ 127 ≡ 1 (mod 7) (2−1)≡ 1 (mod 7)
Lucas-Lehmerova čísla
Lucas, Edouard A.| Lucas, Edouard A., 1842-1891, francouzský matematik. Zabýval se teorií čísel, speciálně Fibonacciho posloupností. Dokázal, že 2127−1 je prvočíslo. |
Čísla Lk, definovaná rekurentně: L2=4, Lk+1=Lk² − 2. se nazývají Lucas-Lehmerova čísla.
Lehmer, Derrick Henry| Lehmer, Derrick Henry , 1905-1991, americký matematik. Zabýval se testováním prvočíselnosti, Lucasovými funkcemi, Bernoulliho čísly, analytickou číselnou teorií, výpočetní technikou,... Zavedl novou metodu rozkladu čísel v součin prvočinitelů s využitím kvadratických zbytků. |
k Lk Mk Lk/Mk ──────────────────────── 1 − 1 − 2 4 3 − 3 14 7 2 4 194 15 − 5 37634 31 1214 6 1416317954 63 −
K zjištění, zda je Mersennovo číslo r=Mk=2k−1
prvočíslem, se používá (pro lichá k) tzv. Lucas-Lehmerův test:
číslo Mk je prvočíslem právě tehdy, když je dělitelem
Lk.
Triviální podsystémy
Nechť d je nejmenší dělitel d\M(n,k) takový, že d ≡ 1 (mod k). Pak R(n,k,r) pro r=M(n,k)/d tvoří triviální podsystem M(n,k). Např: pro n=2:
R(2,2,2): 0 R(2,3,7): 0 R(2,4,5): 0
1 2 1 2 4 1 2 4 3
3 3 6 5 5
7
Čísla r=M(n,k)/d nabývají pro daná n,k následujících hodnot:
n\k│ 2 3 4 5 6 7 8 ───┼───────────────────────── 2 │ 3 7 5 31 7 127 17 3 │ 1 13 5 121 ... 4 │ 5 7 17 ... 5 │ 3 31 .. 6 │ 7 43 .. 7 │ 3 19 .. 8 │ 9 ...
R(7,3,19):
0
1 7 11
2 14 3
4 9 6
5 16 17
8 18 12
10 13 15
19
R(4,4,17):
0
1 4 16 13
2 8 15 9
3 12 14 5
6 7 11 10
17
F-systémy
Předpokládejme systémy R(n,k,r), kde:
r = nh+1
pro hεN.
Tyto systémy budeme nazývat Fermatovými (F) systémy a značit F(n,h). Systém F(n,h) má r+1 instancí {0,..,r}.
Algoritmus pro F-systémy
Algoritmus generování F-systémů je opět tentýž jako u G-systémů či M-systémů - liší se jen v hodnotě r.
Příklady výstupu
F(2,1) F(3,1) F(4,1)
0 0 0
1 2 1 3 1 4
3 2 2 3
4 5
F(2,2) F(3,2) F(4,2)
0 0 0
1 2 4 3 1 3 9 7 1 4 16 13
5 2 6 8 4 2 8 15 9
5 3 12 14 5
10 6 7 11 10
17
F(2,3) F(3,3) F(4,3)
0 0 ....
1 2 4 8 7 5 1 3 9 27 25 19
3 6 2 6 18 26 22 10
9 4 12 8 24 16 20
5 15 17 23 13 11
7 21
14
28
Liché a sudé systémy
0
1 4 3 12 9 10
2 8 6 11 5 7
13
Systémy s lichým a sudým číslem h vytváří v určitém smyslu oddělené skupiny. Pro lichá h totiž platí (n+1)|(nh+1). Liché systémy je proto možné upravit dělením (n+1) - v témže smyslu jako jsme z G-systémů zkostruovali (dělením (n−1)) M-systémy.
Např. v F'(4,3) je r=(4³+1)/(4+1) = 65/5 = 13, viz dále Kummerovy K-systémy.
Pravidla dělitelnosti
Protože v F-systémech je počet transpozic každého vlastního druhu
roven 2k, je v systémech F(2, 2t) roven 2∙2t = 2t+1.
Euler dokázal vztah, který údajně znal již P.Fermat:
d≡1 (mod 2t+1), pro t≥ 0
S jeho pomocí (pro t=5) našel Euler rozklad čísla 4294967297.
Pro t=0,1,2 mají systémy F(2, 2t) tuto strukturu:
F(2,1) F(2,2) F(2,4)
0 0 0
1 2 1 2 4 3 1 2 4 8 16 15 13 9
3 5 3 6 12 7 14 11 5 10
17
Eulerův vztah říká, že každý dělitel čísla r=2(2t)+1 musí mít tvar s∙2t+1 + 1. Tedy každý dělitel musí být tvořen číslem o jedničku větším než je počet instancí v s řádcích.
Počínaje s t=2 mohou druhy tvořit dvojice. E.Lucas si povšiml, že v uvedeném tvaru s∙2t+1 + 1 musí být (pro t≥2) číslo s nutně sudé. Nechť dεP, d>2 je nějaký dělitel čísla F(2,2t). Platí tzv.Lucasův vztah:
d≡1 (mod 2t+2), pro t≥ 2
Každý přirozený dělitel čísla F(2,2t) má tvar s∙2t+2 + 1 (sεN).
| Goldbach, Christian [], 1690-1764, ruský matematik. Věnoval se převážně teorii čísel. Kromě toho se zabýval nekonečnými řadami, teorií křivek a teorií rovnic. |
Goldbachova věta
Každá dvě různá čísla tvaru F(2,2t) tvoří relativní prvočísla, tj. nemají společného dělitele:
(F(2,2t),F(2,2u)) = 1
Kromě toho jsou také čísla F(2,2t) vždy nesoudělná s t, tj.
(t, F(2,2t)) = 1
Jiné
Čísla F(n,2t−2) dávají při dělení 2t vždy
zbytek 2, tj. platí F(n,2t−2) ≡ 2 mod 2t.
Např. F(3,4)=82 ≡ 2 mod 16, F(3,8)=6562 ≡ 2 mod 32, ...
Je-li F(2,2t)εP tak číslo F(3,22t−1) je jím dělitelné.
K-systémy
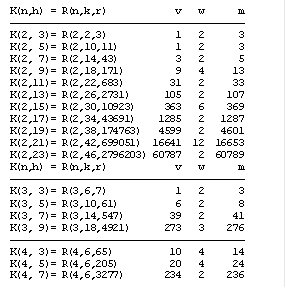
Předpokládejme systémy R(n,k,r), kde:
r = (nh+1)/(n+1)
tyto systémy budeme nazývat Kummerovy (K-) systémy a značit K(n,h).
Obvykle (pro h<r) mají K-systémy řád k=2h a odpovídají systémům R(n,2h,r).Výjimku tvoří systém K(2,3) s řádem k=2(h=r).
Do systémů s prvočíselným r se vnořují právě dva druhy, do systémů se složeným r více druhů.
Např. do K(4,3)= R(4,6,65) se vnořuje R(4,2,5):
n= 4 k= 6 r= 65 n= 4 k= 2 r= 5
0 0
1 4 16 64 61 49 1 4
2 8 32 63 57 33 2 3
3 12 48 62 53 17 5
5 20 15 60 45 50
6 24 31 59 41 34
7 28 47 58 37 18
9 36 14 56 29 51
10 40 30 55 25 35
11 44 46 54 21 19
13 52
22 23 27 43 42 38
26 39
65
C-systémy
Uvažujme systémy R(n,k,r), kde čísla n i r mohou být komplexní. Obecně budeme mluvit o systémech komplexních čísel, C-systémech.
Systémy s komplexním modulem
Systémy s prvočíselným modulem R=a+bi mají stejnou strukturu jako systémy s modulem r, který je normou čísla R, tj. r=a²+b².
V případě r=1+i platí i≡2 mod (1+i):
R(1,1,1+i) R(1,1,2) │ R(i,2,1+i) R(2,2,3)
0 0 │ 0 0
1 1 │ 1 i 1 2
i 2 │ 1+i 3
1+i 3 │
V případě r=2+i je obdobně i≡3 mod (2+i):
R(1,1,2+i) R(1,1,5) │ R(2,4,2+i) R(2,4,5)
0 0 │ 0 0
1 1 │ 1 2 1+i i 1 2 4 3
2 2 │ 2+i 5
i 3 │
1+i 4 │ R(i,4,2+i) R(3,4,5)
2+i 5 │ 0 0
│ 1 i 1+i 2 1 3 4 2
R(1+i,2,2+i) R(4,2,5) │ 2+i 5
0 0
1 1+i 1 4
2 i 2 3
2+i 5
Systém R(i,2,1+i) resp.R(2,2,3)=G(2,2) znázorňuje strukturu komplexních čísel. V první řádku je nulový prvek, v druhém reálná a imagiární jednotka a ve třetím nejmenší komplexní prvočíslo 1+i:
00 0i+0 0 01 10 0i+1 1i+0 1 i 11 1i+1 1+ i
Kvadratické systémy
V systémech se dvěma řádky musí být 1 i −1 vždy v prvním řádku, protože mezi komplexními čísly jsou 1 i −1 druhou mocninou, tedy kvadratickým zbytkem.
R(1+i,2,2+i) R(4,2,5) 0 0 0 1 1+i 1 4 1 −1 2 i 2 3 −i i 2+i 5 0
Komplexně sdružené systémy
Dva systémy R(n1,k,r), R(n2,k,r) nazýváme komplexně sdružené,
jsou-li jejich základy n1 a n2 komplexně sdružené.
Například systémy R(1+i,3,3+2i), R(1−i,3,3+2i):
R(1+i,3,3+2i) R(9,3,13) R(1−i,3,3+2i) 0 0 0 1 1+i 2i 1 9 3 1 1−i −2i 2 −i 1−i 2 5 6 2 i 1+i −1−i −2i −1 4 10 12 −1+i 2i −1 −1+i −2 +i 7 11 8 −1−i −2 −i 3+2i 13 3+2i R(9,3,13): 0 1 2 3 4 5 6 7 8 9 10 11 12 13 R(1+i,3,3+2i): 0 1 2 2i −1−i −i 1−i −1+i +i 1+i −2i −2 −1 3+2i R(1−i,3,3+2i): 0 1 2 −2i −1+i +i 1+i −1−i −i 1−i 2i −2 −1 3+2i
Komplexní jednotky
V každém vlastním řádku systému R(1+i,3,3+2i) je jedna z komplexních jednotek {1,−i,−1,+i}.
R(1+i,3,3+2i) 0 1 1+i 2i +1 ≡ 1 2 −i 1−i −i ≡ 5 −1−i −2i −1 −1 ≡ 12 −1+i −2 +i +i ≡ 8 3+2i
V systému R(9,3,13) těmto jednotkám odpovídají čísla 1,5,12,8, tj. čísla prvního řádku systému R(5,4,13). Protože 5 ≡ −i (3+2i), tak komplexní jednotky najdeme v prvním řádku systému R(−i,4,3+2i):
R(5,4,13) R(−i,4,3+2i) 0 0 1 5 12 8 1 −i −1 +i 2 10 11 3 2 −2i −2 2i 4 7 9 6 −1−i −1+i 1+i 1−i 13 13
Na druhém řádku jsouÿ�ej靀֭nší komplexní sudá čísla a na třetím nejmenší komplexní čísla polosudá.
Moduly G-systémů
Modulem G-systému je v případě nεN číslo r=nk−1. Pro komplexní číslo N=a+bi nedává stejný výpočet smysl. Alespoň ne v tom smyslu, aby vznikající systém byl analogický systému se základem n=a²+b². Např.: Mějme např.n=5, k=3, r= 5³−1 = 124. Podle toho R= (2+i)³−1 = (2+11i)−1 = 1+11i. Ale normou výrazu 1+11i je číslo 122!?
S-systémy
Znaménkové systémy
V znaménkovém systému S(k) je právě tolik druhů jako v G(2,k) po odečtení počtu vzájemně kontrastních druhů (jen rozdílných, ne vnitřně kontrastních).
Platí:
ui (j) = nj ∙ gi nebo ui (j) = nj ∙ (r−gi) (mod r)
Nechť je úroveň instance absolutní hodnota součtu kladných a záporných jednotek, např. −−−++ má úroveň |−1−1−1+1+1| = 1. Pak neutrální druh je druh nulové úrovně.
Přehled instancí systémů S(k)
Druhy Z(k): Instancí Druhů
Úroveň g−čísla druhů transp. celkem v w m neutr.
──────────────────────────────────────────────────────────
k=1:
− 1 0,1 2 1 2
2 1 0 1 0
──────────────────────────────────────────────────────────
k=2:
−− 2 0,3 2 1 2
−+ 0 1,2 1 2 2
2² 1 1 2 1
──────────────────────────────────────────────────────────
k=3:
−−− 3 0,7 2 1 2
−−+ 1 1,3 2 3 6
2³ 1 1 2 0
──────────────────────────────────────────────────────────
k=4:
−−−− 4 0,15 2 1 2
−−−+ 2 1,7 2 4 8
−−++ 0 3 1 4 4
−+−+ 0 5 1 2 2
24 2 2 4 2
Znaménkové systémy s nulou
Přehled instancí systémů S0(k)
System Úroveň Instancí Celkem
─────────────────────────────────────────────────────────
k=1: ( 2 druhů )
0 0 1
− + 0 2
31
─────────────────────────────────────────────────────────
k=2: ( 4 druhů )
00 0 1 *
−+ +− 0 2
0− 0+ −0 +0 1 4
−− ++ 2 2 *
3²
─────────────────────────────────────────────────────────
k=3: ( 6 druhů )
000 0 1 *
0−+ −0+ +0− 0+− +−0 −+0 0 6
00− 00+ 0−0 0+0 −00 +00 1 6
−++ +−− +−+ −+− ++− −−+ 1 6
0−− 0++ −0− +0+ −−0 ++0 2 6
+++ −−− 3 2 *
3³
Systémy mocninných zbytků
Systémy R(n,k,r), kde:
k=κ(r,v) = r div v
budeme pro v>1 nazývat systémy mocninných zbytků.
Specielně v případě v=2 budeme mluvit o kvadratických systémech
(systémech kvadratických zbytků), resp.v případě v=3 o kubických
systémech , apod.
Kvadratické zbytky
Všechna čísla a² mod r se nazývají kvadratické zbytky (zbytky exponentu m=2) podle modulu r. Ostatní čísla (mod r) jsou tzv. kvadratické nezbytky.
Jedním z kvadratických zbytků je vždy nula. Ostatní kvadratické zbytky a nezbytky pro aε(1,r−1), rεP, vznikají symetricky, tj. existuje r div 2 zbytků a r div 2 nezbytků.
Kvadratické zbytky pro r=13:
a² 1 4 9 16 25 36 49 64 81 100 121 144 a² mod 13 1 4 9 3 12 10 10 12 3 9 4 1
K vyhledání kvadratických zbytků není nutné počítat druhé mocniny.
0 1 4 3 12 9 10 2 8 6 11 5 7 13
V systému R(4,6,13) jsou kvadratické zbytky (mod 13) soustředěny v prvním řádku, kvadratické nezbytky v řádku druhém.
Medián
V teorii čísel se používá často hodnota r div 2. Vyskytuje se v mnoha různorodých vztazích a tak si říká o pojmenování. Budeme ji nazývat medián a označíme ji κ(r).
Obecně mediánem řádu s budeme rozumět číslo κ(k,s)=k div s, k,sεN. Pro řád 2 ponecháme jednodušší označení (podobně jako u druhé odmocniny): κ(k)= κ(k,2)= k div 2.
Součin zbytků a nezbytků
Kvadratické zbytky a nezbytky podle rεP pokrývají všechna čísla 1,2,..r−1 a vytvářejí multiplikativní grupy Zr řádu r .
│ zbytky │ nezbytky
│ 1 2 4 │ 3 5 6
───┼──────────┼─────────
1 │ 1 2 4 │ 3 5 6
2 │ 2 4 1 │ 6 3 5
4 │ 4 1 2 │ 5 6 3
───┼──────────┼─────────
3 │ 3 6 5 │ 2 1 4
5 │ 5 3 6 │ 1 4 2
6 │ 6 5 3 │ 4 2 1
Číslo 1 se v tabulce vyskytuje jedině v součinu zbytku se zbytkem nebo nezbytku s nezbytkem.
Jsou-li n a n' dva duální stupně, platí p\(n∙n'−1), tj. n∙n ≡ 1 (mod p).
Proto, když n je kvadratickým zbytkem (mod p), bude jím i n'.
V levém horním kvadrantu tabulky jsou jen kvadratické zbytky.
Grupy kvadratických zbytků
Kvadratické zbytky tvoří pro rεP podgrupy Kr(∙) grup Zr(∙). Řádem těchto podgrup je medián κ(r).
K3 K5 K7 K11 K13
1 1 4 1 2 4 1 3 4 5 9 1 3 4 9 10 12
4 1 2 4 1 3 9 1 4 5 3 9 12 1 4 10
4 1 2 4 1 5 9 3 4 12 3 10 1 9
5 4 9 3 1 9 1 10 3 12 4
9 5 3 1 4 10 4 1 12 9 3
12 10 9 4 3 1
| Carmichael, Robert Daniel [], 1879-1967, matematik. |
Carmichaelova věta
R.D.Carmichael (1905) přeformuloval Wilsonovu větu. Číslo r je prvočíslo, právě když platí:
(κ(r)!)² + (−1)κ(r) ≡ 0 mod r
Wilsonova věta
Wilsonovu větu je také možné přepsat do tvaru:
(−1)κ(r)∙(κ(r)!)² ≡ −1 (mod r)
Sylvester, James Joseph| Sylvester, James Joseph [], 1814-1897, anglický matematik, významný tvůrce nové symboliky. Zabýval se teorií elementárních dělitelů, algebrou forem, teorií determinantů. Spolu s Cayleym vytvořili první algebraickou teorii invariantů kvadratických forem. Věnoval se také mechanice. |
Sylvesterova věta
Sylvester (1860)
∑κ(r,k)∙φ(k) = n∙(n+1)/2
Pro r=5:
k=1 5∙φ(1) = 5
k=2 2∙φ(2) = 2
k=3 1∙φ(3) = 2 5∙6/2 = 15
k=4 1∙φ(4) = 2
k=5 1∙φ(5) = 4
───────
15
Eulerovo kriterium
Pro uεN, rεP označme:
Q(u,r) = uκ(r) mod r
Když r|u tak platí:
Q(u,r)= 0
Např. Q(14,7) = 14³ mod 7 = 0.
Pro kvadratické zbytky platí:
Q(u,r)= 1
────────────────────────────
16 mod 13 = 1 mod 13 =1
46 mod 13 = 4096 mod 13 =1
36 mod 13 = 729 mod 13 =1
126 mod 13 =2985984 mod 13 =1
96 mod 13 = 531441 mod 13 =1
106 mod 13 =1000000 mod 13 =1
|
Pro kvadratické nezbytky platí:
Q(u,r)= −1
─────────────────────────────
26 mod 13 = 64 mod 13 =−1
86 mod 13 = 262144 mod 13 =−1
66 mod 13 = 46656 mod 13 =−1
116 mod 13 =1771561 mod 13 =−1
56 mod 13 = 531441 mod 13 =−1
76 mod 13 = 117649 mod 13 =−1
|
Jestli je číslo u kvadratickým zbytkem nebo nezbytkem poznáme podle hodnoty Q(u,r)=uκ(r) mod r. To je tzv.Eulerovo kriterium. Když Q(u,r)= 1 (resp.−1), je číslo u kvadratickým zbytkem (resp. nezbytkem) podle modulu r. Eulerovo kriterium je jednoduché a obecné, s výhodou je ho možné použít zvláště pro menší čísla r.
Odvození Eulerova kriteria
Číslo u je kvadratickým zbytkem, když existuje takové číslo a, že platí:
a² ≡ u (mod r).
Po umocnění tohoto vztahu na κ(r)=(r−1)/2 dostaneme:
a2(r−1)/2 ≡ ar−1 ≡ uκ(r) (mod r)
Např. pro r=17, u=19, a=11 platí 11² ≡ 19 (mod 17), tedy
19 je kvadratickým zbytkem mod 17. Po umocnění na κ(17)=8:
1116 ≡ 198 ≡ 1 (mod 17).
Eulerovo kriterium plyne z malé Fermatovy věty. Protože ar−1 ≡ 1 (mod r) tak uκ(r) ≡ 1 (mod r) v případě, kdy u je kvadratickým zbytkem,.
V mocninných systémech R(n,k,r) platí nk ≡ 1 mod r (viz Geometrické posloupnosti). Číslo 1 je vždy v prvním řádku, tedy pro n=1 je nκ(r) ≡ 1 mod r. Proto v systémech se dvěma řádky budou nutně v prvním řádku čísla nκ(r) ≡ 1 mod r (tj. kvadratické zbytky) a ve druhém řádku čísla nκ(r) ≡ −1 mod r (tj. kvadratické nezbytky).
Zbytky vyšších stupňů
Bikvadratické zbytky
Např. čísla u=a4 mod 13 pro všechna aε(1,12):
a4 1 16 81 256 625 1296 2401 4096 6561 10000 14641 20736
a4 mod 13 1 3 3 9 1 9 9 1 9 3 3 1
Mezi bikvadratickými zbztky jsou jen čísla, která se vyskytují na první řádku některého systému R(n,κ(r,4),r), např. R(5,4,13). Protože a4 mod r=(a²)² mod r, je bikvadratický zbytek zároveň i zbytkem kvadratickým, což je zřejmé v porovnání s některým R(n,κ(r,2),r), např. s R(4,6,13):
R(5,4,13): R(4,6,13):
0 0
1 3 9 1 4 3 12 9 10
2 6 5 2 8 6 11 5 7
4 12 10 13
7 8 11
13
Gaussovy třídy
Při analýze bikvadratických zbytků rozděluje Gauss čísla do 4 tříd A,B,C,D podle následujícího schematu:
A │ 1 g4 g8 ... │ bikvadratické zbytky
B │ g g5 g10 ... (mod r) │ nezbytky
C │ g² g6 ... │ kvadratické zbytky
D │ g³ g7 ... │ nezbytky
kde g je takové číslo, že všechna čísla 1,g,...gr−1 jsou (mod r) navzájem různá (viz primitivní kořeny čísla r).
Např. pro r=17, g=3 (vpravo s čísly ve třídách řazenými podle velikosti)
A 1 13 16 4 A 1 4 13 16
B 3 5 14 12 i.e. B 3 5 12 14
C 9 15 8 2 C 2 8 9 15
D 10 11 7 6 D 6 7 10 11
Rozložení čísel ve třídách odpovídá rozložení instancí v R-systému, v našem příkladě R(4,4,17):
R(4,4,17)
0
1 4 16 13 │ A (1)
2 8 15 9 │ C (g²=9)
3 12 14 5 │ B (g=3)
6 7 11 10 │ D (g³=27≡10)
17
Vztahy tříd
Součin libovolného čísla z třídy C (např.9 mod 17) násobený číslem z třídy D (např.7 mod 17) dává výsledek patřící do třídy B (9∙7=63≡12 mod 17). Obecně platí pro násobení tříd následující tabulka:
│ A B C D Z4+│ 0 1 2 3
──┼───────────── ──┼────────────
A │ A B C D 0 │ 0 1 2 3
B │ B C D A 1 │ 1 2 3 0
C │ C D A B 2 │ 2 3 0 1
D │ D A B C 3 │ 3 0 1 2
Tabulka odpovídá tabulce sčítání čísel v oboru Z4 (viz Grupy).
Komplexní jednotky
Při řešení problému bikvadratických zbytků použil Gauss komplexní
čísla. Třídám A,B,C,D přiřadil komplexní jednotky 1,i,−1,−i.
Označme třídy A,B,C,D čísly (charaktery) c=0,1,2,3 a čísla (instance) ve
třídách písmenem u. Platí:
uκ(r,4) ≡ ic mod r
kde i je imaginární číslo, i=√−1.
Středy multiplikativních tabulek
k=2: k= 3: k = 4: k = 5: k = 6:
1 1 2 1 2 3 1 2 3 4 1 2 3 4 5
2 1 2 0 2 2 4 1 3 2 4 0 2 4
3 2 1 3 1 4 2 3 0 3 0 3
4 3 2 1 4 2 0 4 2
5 4 3 2 1
Uprostřed multiplikativních tabulek (mod k) je buď jedno jediné číslo (když k je sudé) nebo čtveřice čísel (když k je liché). Čtveřice čísel obsahuje čísla κ(k)² mod k a κ(k)∙(κ(k)+1) mod k.
Pro sudá k:
· Pro k=4s (tj. k je dělitelné čtyřmi) je uprostřed tabulky nula.
·
Pro k=4s−2 je uprostřed tabulky číslo 2s−1.
Např. pro k=6 (s=2) je uprostřed tabulky číslo 3 (tj. 2∙2−1).
Pro lichá k:
· Pro k=4s−1 tvoří vnitřní čtveřici čísla s a 3s−1.
· Pro k=4s+1 tvoří vnitřní čtveřici čísla s a 3s+1.
| Čísla uprostřed multiplikativních tabulek (mod k) nezávisí jen na čísle k, ale také na jeho příslušnosti do některé ze 4 tříd: 4s−1, 4s, 4s+1 a 4s+2. |
Liché číslo n je ryzí, pokud i jeho medián κ(n) je lichý. Ryzí lichá čísla (p,q,...):
· netvoří čtverec, tj.druhá mocnina druhá mocnina má vždy tvar 4s nebo 4s+1
· prvočísla z množiny ryzích lichých čísel (tzv. Gaussova prvočísla) jsou v komplexním oboru nerozložitelná (např. 3,7,11,19,23,31,43,47,59,67,71,79,83,...)
· kongruence x²+y²≡0 (mod p) není řešitelná (pεP)
· číslo aεN se dá vyjádřit jako součet dvou nesoudělných čtverců, jedině když v rozkladu není žádné ryzí liché prvočíslo
Neryzí lichá čísla (p,q,...) mají následující vlastnosti:
· tvoří čtverec, tj.(2k+1)² má vždy tvar 4s+1
·
Euler dokázal, že prvočísla tvaru 4s+1 jsou vždy jednoznačným
součtem dvou čtverců
(např. 1=0+1, 5=1+4, 13=4+9, 17=1+16, 29=4+25, 37=1+36, 41= 16+25, 53=
4+49, 61=25+36, 73= 9+64, 89=25+64, 97= 16+81, 101= 1 +100)
· prvočísla, která nejsou ryzími lichými čísly jsou v komplexním oboru rozložitelná (např. 5=(2+i)(2−i), 13=(3+2i)(3−2i),...)
· některá z tzv.dokonalých čísel, tj. čísel, která jsou součtem všech svých dělitelů, se dají podle Eulera vyjádřit ve tvaru pq∙N², kde p i q jsou neryzí lichá čísla.
· pro r = 4s+1εP dostává Carmichaelova věta tvar:
(κ(r)!)² = −1 mod r
Eulerovy třídy
Euler dokázal, že na třídách (mod 4) závisí i některé složitější
výrazy.
Nechť (a1,b1)=1, (a2,b2)=1 a čísla p1,p2 ε P Označme f(a,b) =
a²+n∙b².
Když p1 ≡ p2 (mod 4n) a p1 | f(a1,b1) pak také p2 | f(a2,b2).
Např.
pro n=1: 5|(1+4), 13|(4+9) a 5 ≡ 13 (mod 4);
nebo 13|(1+25), 17|(9+25) a 13 ≡ 17 (mod 4).
pro n=2: 11|(4+2∙9), 59|(9+2∙25) a 11 ≡ 59 (mod 8).
Zbytky exponentu v
Uvažujme R-systémy (rεP), které mají právě v vlastních řádek. Vlastním řádkem přitom budeme rozumět řádek, který má právě k instancí (řádky 0 a r nejsou vlastní, ale vnořené). Takové systémy mají řád k=r div v = κ(k,v).
Přitom v prvním řádku nacházíme zbytky exponentu v, tj. tzv. v-tické zbytky (pro v=2 kvadratické zbytky, v=3, kubické zbytky,...). V ostatních řádcích jsou nezbytky (exponentu v).
Např. kubické zbytky, tj. čísla u=a³ mod r jsou na prvním řádku schemat R(n,κ(r,3),r):
Pro r=7: Pro r=13:
a3 1 8 27 64 125 216 a3 1 8 27 64 125 216 343 512 729
a3 mod 7 1 1 6 1 6 6 a3 mod 13 1 8 1 12 8 8 5 5 1
R(6,2,7): 0 R(5,4,13): 0
1 6 1 5 12 8
2 5 2 10 11 3
3 4 4 7 9 6
7 13
Eulerovo zobecněné kriterium
Systémy s v vlastními řádky, mají řád k=r div v = κ(r,v), tj.
zapíšeme je R(n,κ(r,v),r).
Např. R(5,4,13) má 3 vlastní řádky, tj. v=3 a řád k=13 div 3 = 4.
R(5,4,13):
0
1 5 12 8
2 10 11 3
4 7 9 6
13
Číslo u je v-tickým zbytkem, když existuje takové a, že platí av ≡ u (mod r).
Po umocnění tohoto vztahu na κ(r,v):
av(r−1)/v ≡ ar−1 ≡ uκ(r) (mod r).
Dostáváme obdobný vztah jako v předchozím odstavci. Číslo u je v-tickým zbytkem, když je Qv(u,r)= 1, přičemž:
Qv(u,r) = uκ(r,v) mod r.
Legendreovy systémy
Číslo u je v-tickým zbytkem (mod r), když leží v prvním řádku
systému R(n,k,r), kde k=κ(r,v) (viz Eulerovo zobecněné kriterium).
V případě u=v, je číslo u je samo o sobě u-tickým zbytkem. Systémy
R(n,k,r), které mají v vlastních řádek a ve kterých zároveň v prvním
řádku leží číslo v, nazveme Legendreovy systémy.
0 1 2 4 │ v = 2 3 6 5 │ 7 ── k=3 ──
Např. R(2,3,7) je Legendreův systém: má 2 vlastní řádky a v prvním řádku číslo 2 (číslo 2 je kvadratickým zbytkem mod 7). Platí: 2³ ≡ 1 (mod 7).
Obecně podle Eulerova kritéria musí být Qv(v,r) = vκ(r,v) mod r = 1, kde v exponentu je řád systému: k=κ(r,v). Proto v Legendreových systémech R(n,κ(r,v),r) platí:
vk ≡ 1 (mod r)
Legendre, Adrien-Marie| Legendre, Adrien-Marie, , [ležándr] 1752-1833, francouzský matematik a fyzik. Výrazně ovlivnil další vývoj teorie čísel: objevil kvadratický zákon reciprocity a zobecnil vztahy týkající se velké Fermatovy věty. Zabýval se také elipsoidy, eliptickými funkcemi a integrály. Spolupracoval na zaměření Země, odvodil nové vztahy pro sférické trojúhelníky. Řídil sestavování logaritmických a trigonometrických tabulek. |
Hodnota kk (mod r)
Protože k=κ(r,v), je k∙v = r−1 (rε P). Tedy (r−1)k = (v∙k)k = kk∙vk, přičemž:
· vk ≡ 1 (mod r)
· (r−1)k ≡ (−1)k (mod r).
Po dosazení dostáváme:
kk ≡ (−1)k (mod r)
Systémy se sudým řádem
Když k je sudé (k=2t) tak (−1)k = 1 platí:
v²t ≡ (2t)2t ≡ 1 (mod r)
Zde r= 2tv+1, rε P.
Např. pro t=1,2,3,4 dostáváme hodnoty:
t (2t)2t rozklad T=(2t)2t−1
────────────────────────────────────────────────
1 2² = 4 3
2 44= 256 255 = 3∙5∙17
3 66 = 46656 46655 = 5∙7∙31∙43
4 88 = 16777216 16777215 = 3²∙5∙7∙13∙17∙241
Rozklad čísla T napovídá možnosti pro volbu čísla r. Odvodíme pro každé t jeden vhodný Legendreův systém se sudým řádem:
t=1 r= 3, v= 1, k=2
0
1 2
3
t=2 r=17, v= 4, k=4
0
1 4 16 13
2 8 15 9
3 12 14 5
6 7 11 10
17
|
t=3 r=31, v= 5, k=6
0
1 6 5 30 25 26
2 12 10 29 19 21
3 18 15 28 13 16
4 24 20 27 7 11
8 17 9 23 14 22
31
t=4 r=17, v= 2, k=8
0
1 2 4 8 16 15 13 9
3 6 12 7 14 11 5 10
17
|
Systémy primitivních kořenů
Systémy R(n,k,r), kde:
k=r−1
budeme nazývat systémy primitivních kořenů.
Systémy primitivních kořenů zastupují případ v=1 systémů mocninných
zbytků.
Primitivní kořeny
Mocniny určitého kořenu mohou projít všemi ostatními kořeny jedině v případě, když s=h, tj. když řád (s) daného kořenu je roven exponentu binomické rovnice h.
Kořeny s touto vlastností nazýváme primitivní kořeny . Základní kořen α je vždy jedním z primitivních kořenů.
Mezi systemy R(n,k,r) (pro rεP) vybereme takové, které mají r−1 transpozic, tj. ve kterých se (až na čísla 0 a r) nezalamují řádky. Pro r=7 existují 2 takové systémy, R(3,6,7) a R(5,6,7):
R(3,6,7): R(5,6,7):
0 0
1 3 2 6 4 5 1 5 4 6 2 3
7 7
Každý z těchto systémů má právě jeden vlastní druh s reprezentantem g=1. Pro α=n, j=0,..,r−1 prochází výrazy αj všechny instance a tvoří tak celočíselnou analogii primitivních kořenů rovnice x6−1=0 s exponentem h=r−1=6.(Viz cyklické grupy,...)
Počet primitivních kořenů je roven počtu čísel nesoudělných s exponentem h. Binomická rovnice xh−1 = 0 má proto φ(h) primitivních kořenů. Pro dané rεP existuje vždy φ(r−1) systémů, jejichž základem n je primitivní kořen. Např. při r=7 existují φ(6)= 2 primitivní kořeny.
Rozmístění primitivních kořenů
Kořen xj(h) je primitivním kořenem rovnice xh−1=0 tehdy, když čísla j a h jsou nesoudělná, (j,h)=1. S číslem h=6 jsou nesoudělná čísla j=1 resp. 5:
j: 0 1 2 3 4 5
────────────────────────────────────
R(3,6,7): 1 3 2 6 4 5
R(5,6,7): 1 5 4 6 2 3
Pro r=11 existují φ(10)= 4 primitivní kořeny a tedy čtyři různé systémy s plným počtem transpozic:
R(2,10,11): R(6,10,11): 0 0 1 2 4 8 5 10 9 7 3 6 1 6 3 7 9 10 5 8 4 2 11 11 R(7,10,11): R(8,10,11): 0 0 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 11 11
Primitivní kořeny 2,6,7,8 najdeme na pozicích 1,3,7,9, tj. na pozicích čísel nesoudělných s číslem r−1=10.
0 1 2 3 4 5 6 7 8 9
───────────────────────────────────────────────────────
R(2,10,11): 1 2 4 8 5 10 9 7 3 6
R(6,10,11): 1 6 3 7 9 10 5 8 4 2
R(7,10,11): 1 7 5 2 3 10 4 6 9 8
R(8,10,11): 1 8 9 6 4 10 3 2 5 7
Pro r=13 existují φ(12)= 4 primitivní kořeny: 2,6,7,11. Tyto kořeny tvoří základy systémů R(2,12,13), R(6,12,13), R(7,12,13) a R(11,12,13).
R(n,k,13) 0 n │ k +−> 1 2 4 8 3 6 12 11 9 5 10 7 R(2,12,13) ────┼──── │ 13 1 │ 1 │ 2 │ 12 ──┼ 0 3 │ 3 +−> 1 6 10 8 9 2 12 7 3 5 4 11 R(6,12,13) 4 │ 6 │ 13 5 │ 4 │ 6 │ 12 −+ 0 7 │ 12 ───> 1 7 10 5 9 11 12 6 3 8 4 2 R(7,12,13) 8 │ 4 13 9 │ 3 10 │ 6 0 11 │ 12 ───> 1 11 4 5 3 7 12 2 9 8 10 6 R(11,12,13) 12 │ 2 13
Kritérium pro primitivní kořeny
Nechť r je liché prvočíslo (tj. rεP, r>2).
Podle malé Fermatovy věty je nr−1 ≡ 1 mod r, tj. r |(nr−1−1). Pokud r je liché je číslo r−1 sudé a můžeme rozepsat výraz nr−1−1 podle vzorce a²−b² = (a−b)(a+b):
nr−1−1 = (nκ(r) −1)(nκ(r) +1)
Rozdíl součinitelů je 2, nemohou mít tedy většího společného dělitele než 2. Číslo r musí být proto dělitelem jen jednoho z čísel (nκ(r) −1) nebo (nκ(r) +1). Dělitelem (nκ(r) −1) ale být nemůže − muselo by být nκ(r) ≡ 1 mod r, což u primitivního kořenu n není možné (na indexu κ(r) by se musel zalomit řádek...)
Pro primitivní kořen n (podle modulu r) platí:
nκ(r) ≡ −1 mod r
Primitivní kořeny splňují tentýž vztah jako kvadratické nezbytky (viz Eulerovo kriterium). Ne všechny kvadratické nezbytky jsou primitivními kořeny, primitivní kořeny tvoří podmnožinu kvadratických nezbytků.
Monocykly
Posloupnost čísel B1,B2,....Bn,A1,A2,..An můžeme přerovnat na posloupnost A1,B1,A2,B2,... pomocí jedné permutace. Vzniká otázka, kdy má tato permutace, právě jen jeden cyklus. (tzv. úloha "perfect shuffle" v teorii třídících algoritmů).
Uvažujme ekvivalentní úlohu: řadu 2n čísel 0,1,..,2n−1 máme přeskupit jednou permutací tak, aby se n lichých čísel předřadilo n číslům sudým. Zajímá nás pro která n je takové přeskupení možné uskutečnit permutací s jedním cyklem (monocyklem).
Monocyklus existuje jedině tehdy, když číslo 2 je primitivním kořenem podle modulu p=2n+1.
Příklad monocyklu
Pro n=5 (p=11) má permutace jediný cyklus [0 1 3 7 4 9 8 6 2 5]:
j 0 1 2 3 4 5 6 7 8 9
i 1 3 5 7 9 0 2 4 6 8
Vznik cyklu:
j 0 1 2 3 4 5 6 7 8 9 2j−1 0 1 3 7 15 31 63 127 255 511 (2j−1) mod 11 0 1 3 7 4 9 8 6 2 5
Cyklus má plnou délku protože neexistuje j<p−1 takové, že (2j−1) mod p=0.
Příklad více cyklů
Pro n=3 (p=7) je permutace složená ze dvou cyklů [0 1 3][2 5 4]:
Permutace: Vznik cyklu:
j 0 1 2 3 4 5 j 0 1 2 3 4 5
i 1 3 5 0 2 4 2j−1 0 1 3 7 15 31
(2j−1) mod 7 0 1 3 0 1 3
permutace netvoří monocyklus: cyklus nemá plnou délku, protože (2³−1) mod 7 = 0.
Briggs Rafael| Briggs Rafael, 1526-1572, anglický matematik, publikoval první tabulku desítkových logaritmů. |
Logaritmická funkce
Zvláštním význam v matematice má (pro P=ap, Q =aq, a,p,q,P,Q,r ε R)
· exponenciální funkce , která převádí operaci sčítání na násobení:
PQ = ap aq = ap+q
např. 5∙125=51 5³ = 51+3= 54 = 625, a
Neper(Napier) John| Neper(Napier) John , 1550-1617, skotský matematik, objevitel přirozených logaritmů. Zabýval se sférickou trigonometrií a výpočetními metodami. |
logaPQ =logaP+logaQ = p+q
Opakované sčítání logaritmů (násobením logaritmu číslem...):
logaPv = v logaP = vp
např. log5625 = log554 = 4∙ log55 = 4.
Základ a se volí podle okolností:
· V desítkové soustavě je výhodný základ a=10, tomu odpovídají desítkové (dekadické) logaritmy.
· V hudbě jsou tóny v poměru 2:1 (oktáva) vnímána obdobně. V tom případě je vhodné použít dvojkové logaritmy se základem a=2. Tyto logaritmy se používají také např. v teorii informací.
· V matematické analýze má výsadní postavení Eulerovo číslo e=(1+1/n)n (čím vyšší n, tím přesnější e). Eulerovo číslo je základem přirozených logaritmů a=e (popř.a=1/e, jak původně zavedl J.Napier).
· V teorii čísel se používají celočíselné logaritmy. Vhodnými základy jsou v tomto případě tzv. primitivní kořeny.
Celočíselné logaritmy
Uvažujme exponenciální funkci: y=nx mod r, která
transpozici xε{0..r−2} přiřazuje určité číslo {1..r−1}.
K funkci existuje inverzní funkce analogická funkci logaritmické: x=
ind(y) mod (r−1). Přiřazení je oboustranně jednoznačné právě tehdy, když
n je primitivní kořen. Když modulem exponenciální funkce je r pak modulem
funkce inverzní je (r−1).
Např. pro r=11, n=2:
x 0 1 2 3 4 5 6 7 8 9
y=nx mod r 1 2 4 8 5 10 9 7 3 6
y 1 2 3 4 5 6 7 8 9 10
x=ind(y) mod r−1 0 1 8 2 4 9 7 3 6 5
Některé kongruence je možné řešit obdobně jako logaritmické
rovnice:
Např. a³≡9 (mod 11):
a³ ≡ 9 (mod 11)
ind(a³) ≡ 3∙ind(a) ≡ ind(9) (mod 10)
ind(a) ≡ ind(9)/3 ≡ 6/3 ≡ 2(mod 10)
a ≡ 4 (mod 11) Zkouška: 4³ mod 11 = 64 mod 11 = 9
Z kritéria pro primitivní kořeny plyne, že indexem čísla −1 (mod r)
je κ(r).
Např. pro r=11:
y
1 2 3 4 5 6 7 8 9 10
x=ind(y) mod (r−1) 0 1 8 2 4 9 7 3 6 5
ind(−1)= ind(r−1)= ind(10) = 5 κ(r) = 11
div 2 = 5.
Součin primitivních výrazů
Mezi R-systémy s r=5 jsou φ(4)= 2 systémy primitivních kořenů:
R(2,4,5) 0 R(3,4,5) 0
1 2 4 3 1 3 4 2
5 5
Primitivními výrazy r(x) nazveme polynomy, jejichž koeficienty jsou instancemi systémů primitivních kořenů.
r1(x)= 1+2x+4x²+3x³ r2(x)= 1+3x+4x²+2x³
Zajímat nás bude součin všech takových výrazů pro dané r za
předpokladu, že xr−1=xk=1. Pro r=5 je:
r1(x)∙r2(x) = 5(6+5x+4x²+5x³)
Za předpokladu, že každý výraz V(x) můžeme nahradit výrazem V(x) mod r je
dále: [r1(x)∙r2(x)]5 =
5(1−x²).
(Ve výpočtu součinů se objevuje výraz ∑s² pro s=1,..,p−1 a ten
je vždy dělitelný p protože ∑s² = (p−1)p(2p−1)/6,...).
Pro r=7 je:
r1(x)= 1+3x+2x²+6x³+4x4+5x 5
r2(x)= 1+5x+4x²+6x³+2x4+3x5
r1(x)∙r2(x) = 7(13+10x+11x²+8x³+11x4+10x5
a [r1(x)∙r2(x)]7 = 7(1−x³)(−1+3x−3x²).
Takové výrazy,po dosazením x=α, kde α je komplexní kořen rovnice xr=1, souvisí s Kummerovou teorií cyklických čísel.
W-systémy
Systémy R(n,k,r), kde:
r = t²
a tεN budeme nazývat Wieferichovými (W) systémy. Specielně nás bude zajímat případ, kdy n=2 a t je liché prvočíslo (tεP).
Pokusíme se nahlédnout, jaké vlastnosti mají W-systémy v případě, kdy t je tzv.Wieferichovo prvočíslo.
W-systémy - Příklady výstupu
R(2, 20, 5²)
0
1 2 4 8 16 7 14 3 6 12 24 23 21 17 9 18 11 22 19 13
5 10 20 15
25
R(2, 21, 7²)
0
1 2 4 8 16 32 15 30 11 22 44 39 29 9 18 36 23 46 43 37 25
3 6 12 24 48 47 45 41 33 17 34 19 38 27 5 10 20 40 31 13 26
7 14 28
21 42 35
49
| Wieferich, Arthur [], 1884-1954, německý matematik a pedagog. Dokázal, že platnost Velké Fermatovy věty mohou v první případě narušit nanejvýše jen některá (tzv.Wieferichova) prvočísla |
Wieferichova prvočísla
Wieferichovo prvočíslo je takové p , pεP, že platí:
2p -1 ≡ 1 (mod p2)
Jediná dosud známá Wieferichovo prvočísla jsou 1093 a 3511.
Řády W-systémů
Řády k W-systémů jsou v pozorovaných případech (t=3,5,7,..) vesměs větší než je hodnota t, tedy k>t (například k=20 pro t=5; k=21 pro t=7; ...) .
Dokonce platí, že t | k (v našem příkladě 5 | 20; 7 | 21). Přitom řád k nabývá často hodnoty k = t(t-1), tedy k | t(t-1) (například 20 | 5*4, 21 | 7*6).
V systému R(n,k,t²) musí číslo W=2t-1 - 1 mod t² ležet v prvním řádku, přičemž tím určuje řád systému k a platí k | (t-1).
Zde je tedy hlavní odlišnost systémů R(n,k,t² ) s běžným prvočíslem t od systémů s Wieferichovým prvočíslem t.
V prvním případě k | t(t-1), ale v druhém musí být k nutně menší, tedy: k | (t-1).
Systém R(2, 364, 1093²)
V systému řádu k = 364 je m=3284 druhů, z toho v=3282 vlastních a w=2 vnořené (z řádu 1).
Celkem tedy systém obsahuje 3282*364 + 2* 1 = 1194650 instancí (=1093²+1).
Systém R(2, 1755, 3511²)
V systému řádu k =1755 je m=7026 druhů, z toho v=7024 vlastních a w=2 vnořené (z řádu 1).
Celkem tedy systém obsahuje 7024*1755 + 2* 1 = 12327122 instancí (=3511²+1).
Vnořování ve W-systémech
Řád každého systému di vnořeného do R(n,k, t² ) musí dělit vlastní řád k, tedy di | k, přičemž o vnořování rozhoduje společný dělitel 2d-1 a t² .
Pro prvočíselné tεP je jedinou možností, aby bylo (2d-1, t² )>1 případ t | 2d-1 pro nějaké di | k.
V R(2, 20, 5²) je k= 2² *5 a pro d=5 platí t | 25-1. V R(2, 20, 7²) je k=3*7 a pro d=3 platí t | 2³-1.
Proto mají tyto systémy vnořené druhy s k/t transpozicemi.
V případě, kdy pro všechna di | k platí (2d-1, t² )=1, má systém jen vlastní druhy a triviální druhy vnořené z řádu d=1.
Protože triviální druhy jsou vždy 2 a celkový počet instancí je t²+1, připadá na vlastní druhy t²-1 instancí.
Každá vlastní instance má k transpozic, tedy k |
t²-1.
Tak je to také v obou výše uvedených systémech -
v R(2, 364, 1093²) platí 364
|
1093²-1
v
R(2, 1755, 3511²) platí 1755 |
3511²-1.
Malá Fermatova věta
V systémech R(n,k, t² ) je 2t-1 = a* t² + h (a,hεN), kde h=1 v případě, že t je Wieferichovo prvočíslo.
V jiných případech dostáváme - např. pro t=5: h=16, pro t=7: h=15, ... přičemž platí: h mod t = 1.
A tedy h = b*t + 1 (bεN). Spojením s předcházejícím vztahem dostáváme:
2t-1 = a* t² + b*t + 1
Je zřejmé, že celá rovnice je dělitelná t jedině v případě, že t | 2t-1 -1.
Obecnější případ
Rovnici 2t-1 = a* t² + b*t + 1 splňují v případě b=0 Wieferichova prvočísla 1093 a 3511.
Pro další hodnoty b = 1,2,... dostáváme následující čísla t.
b=1: 3,29,37,3373; b=2: 7,71,379; b=3: 13,19,173; b=5: 11; b=6: 31, 89; ...