F-součty v posloupnostech
Nyní vezměme obecnější problém. Hledejme všechny (aritmetické) posloupnosti
f = {f(i)} v nichž existují takové členy f(a),f(b),f(c), že platí tzv. F-součet: f(a)+f(b)=f(c).
.
Fermatova věta pouze redukuje obor posloupností na f(n) = nk (k je konstanta), tj. na hledání F-součtu ak +bk =ck.
Základní pojmy
Aritmetické posloupnosti
Posloupnost {f(t)} se nazývá aritmetická posloupnost k-tého řádu, jestliže její k-tá rozdílová posloupnost je konstantní.
Aritmetické posloupnosti tvoří algebraické funkce
s konstantními exponenty (lineární a mocninné funkce,...).
Když {d(t)} je rozdílová posloupnost posloupnosti {f(t)},
nazýváme {f(t)} součtovou posloupností posloupnosti {d(t)}.
Charakteristiky
Množinu prvních členů jednotlivých rozdílových posloupností (konstantní posloupností počínaje) nazveme charakteristikou posloupnosti.
Každá posloupnost s definovaným počátečním prvkem má právě jednu charakteristiku.
Např. posloupnost třetích mocnin je třetího řádu s charakteristikou [6,6,1,0]:
0, 1, 8, 27, 64, 125, 216, 343, 512, 729, ...
1, 7, 19, 37, 61, 91, 127, 169, 217, ...
6, 12, 18, 24, 30, 36, 42, 48, ...
6, 6, 6, 6, 6, 6, 6, 6, ...
Charakteristiku budeme vypisovat zdola, tj. od konstantní posloupnosti. Z důvodu jednoduššího zápisu některých vztahů, ale zachováme číslování shora.
Prvky charakteristiky {r(h)} jsou ... r2,r1,r0. V našem příkladě [6,6,1,0] je r0=0,r1=1,r2=6,r3=6.
Členy posloupnosti D, která vznikne z charakteristiky, která je součtem (rozdílem) charakteristik daných posloupností RD= RA + RB, jsou součtem (rozdílem) příslušných členů daných posloupností, tj. D=A+B.
Charakteristiky posloupností různých řádů se sčítají zprava,
přičemž na chybějící místa vlevo se doplňují nuly.
Např.součtem charakteristik [6,6,1,0] posloupnosti A=f(t) = t³ a [2,1,0] posloupnosti B=g(t) = t²
je charakteristika RD=[6,8,2,0] posloupnosti D=f(t)+g(t)=t³+t²:
Charakter. Posloupnost
─────────────────────────────────────────────
RA= [6,6,1,0] A= {0,1, 8,27,64,125,216,... }
RB= [0,2,1,0] B= {0,1, 4, 9,16, 25, 36,... }
─────────────────────────────────────────────
RD= [6,8,2,0] D= {0,2,12,36,80,150,252,... }
Elementární posloupnosti
Nulová posloupnost, tj. posloupnost {0,0,0,0,0,...} má všechny rozdílové posloupnosti nulové. Může proto zastupovat posloupnosti libovolného řádu, tj. posloupnosti s charakteristikami [0],[0,0],[0,0,0], atd.
Základní posloupností řádu k nazýváme posloupnost s charakteristikou tvaru: [1,0,0...,0,r(0)], tj. s jednotkovou konstantou u poslední rozdílové posloupnosti (tj.r(k)=1) a nulovým posunem u dalších rozdílových posloupností (tj. pro h ε <1,k−1> je r(h)=0). Číslo r(0) rozlišuje jednotlivé základní posloupnosti.
Pro k=0..5 jsou charakteristikami
základních posloupností:
• k=0: [1]
• k=1: [1,r0]
• k=2: [1,0,r0]
• k=3: [1,0,0,r0]
• k=4: [1,0,0,0,r0]
• k=5: [1,0,0,0,0,r0]
Pro každý F-součet (a,b,c) je možné z nulové posloupnosti daného řádu vytvořit základní posloupnost [1,0,...0,rk]. Do nulové posloupnosti se promítá nekonečný počet základních posloupností.
Základní posloupnosti jsou snadno čitelné a sestavitelné. Nejsou ale v celém rozsahu rostoucí - jejich první 2 členy jsou stejné. Proto nyní zavedeme ještě další typ posloupností... Výchozí posloupností řádu k nazýváme posloupnost s charakteristikou tvaru: [1,1,1...,1,r(0)].
Pro k=0..5 jsou charakteristikami
výchozích posloupností:
• k=0: [1]
• k=1: [1,r0]
• k=2: [1,1,r0]
• k=3: [1,1,1,r0]
• k=4: [1,1,1,1,r0]
• k=5: [1,1,1,1,1,r0]
Záměnné posloupnosti
Posloupnosti nazýváme záměnné, pokud jsou identické, až na očíslování svých členů. Např. posloupnosti s charakteristikami [6,6,1,0] a [6,0,1,−1] jsou záměnné.
Charakter. Posloupnost
─────────────────────────────────────────────
[6,6,1,0] { 0,1,8,27,64,125,216,... }
[6,0,1,−1] {−1,0,1, 8,27, 64,125,216,.}
Obecněji jde v tomto příkladě o všechny posloupnosti [6,6(m+1),3m²+3m+1, m³]; (zde speciálně pro m=0, resp.−1).
F-posloupnosti
Existují-li v posloupnosti {f(n)} = f(0),f(1),f(2),... čísla f(a),f(b),f(c) taková, že platí f(a)+f(b)=f(c), mluvíme o F-součtu.
F-součet označujeme trojicí F-indexů (a,b,c), 1≤ a < b < c.
V následující tabulce jsou vypsány posloupnosti s charakteristikami [6,6,1,0..8], jejich první existující F-součet (v prvních 100 členech posloupnosti) a příslušné F-indexy.
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,6,1,0] {0,1,8,27,64,125,… }
[6,6,1,1] {1,2,9,28,65,126,… } ( 6, 8, 9) 217+513=730
[6,6,1,2] {2,3,10,29,66,127,…} ( 5, 6, 7) 127+218=345
[6,6,1,3] {3,4,11,30,67,128,…}
[6,6,1,4] {4,5,12,31,68,129,…}
[6,6,1,5] {5,6,13,32,69,130,…}
[6,6,1,6] {6,7,14,33,70,131,…} (43,58,65) 79513+…=274631
[6,6,1,7] {7,8,15,34,71,132,…} ( 0, 1, 2) 7+8=15
[6,6,1,8] {8,9,16,35,72,133,…} (12,16,18) 1736+4104=5840
Např. V posloupnosti {7,8,15,34,71,132,223,...} je třetí člen (15) součtem předchozích dvou (7+8).
Posloupnosti, v nichž existuje F-součet nazveme F-posloupnosti.
Násobky posloupností
Nechť posloupnost f'(n) je q násobkem posloupnosti f(n), tj. f'(n)=q∙f(n).
Charakteristika R' posloupnosti f'(n) je q-násobkem charakteristiky R, tj. r'(m)=q∙r(m), mεN, qεN.
Existuje-li v posloupnosti f(n) F-součet s indexy (a,b,c), existuje F-součet (s týmiž indexy) i v posloupnosti a'(n).
Např.F-součet s indexy (0,2,5) existuje ve všech posloupnostech s charakteristikami [1,0,9], [2,0,18], [3,0,27], [4,0,36],...
Charakter. Posloupnost F-indexy F-součet
───────────────────────────────────────────────────────────
[1,0,9] {9,9,10,12,15,19,24,...} ( 0, 2, 5) 9+10=19
[2,0,18] {18,18,20,24,30,38,48,.} ( 0, 2, 5) 18+20=38
[3,0,27] {27,27,30,36,45,57,72,.} ( 0, 2, 5) 27+30=57
[4,0,36] {36,36,40,48,60,76,96,.} ( 0, 2, 5) 36+40=76
Je-li posloupnost f(n) F-posloupnost, pak F-posloupnosti jsou i všechny posloupnosti f'(n), pro qεN.
Posloupnosti se stejnými F-indexy
V množině všech posloupností existuje pro dané F-indexy (a,b,c) celá třída posloupností s odpovídajícími F-součty.
Jinými slovy: ke každému F-součtu dané posloupnosti existuje analogický F-součet také v jiných posloupnostech.
Ukazuje se, že:
- Nulová posloupnost obsahuje všechny možné F-součty.
- Existují posloupnosti, které obsahují nekonečný počet F-součtů (např. posloupnost f(n) = n²).
- Existují posloupnosti, které neobsahují ani jeden F-součet (např. posloupnost f(n) = n³).
- Dva dané F-součty mohou existovat i ve více posloupnostech. Tedy transformací 2 různých F-součtů z jedné posloupnosti nemusíme dostat vždy 2 různé posloupnosti.
Např. F-součty s indexy (6,8,10) a (5,12,13) existují v obou posloupnostech: s charakteristikou [2,1,0] i [1,0,2].
Charakter. Posloupnost
─────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,144,169..}
[1,0,2] {2,2,3,5, 8,12,17,23,30,38, 47, 57, 68, 80..}
V [2,1,0] je 36+64 = 100 a v [1,0,2] je pro stejné indexy 17+30=47. Obdobně 25+144 = 169 a 12+68=80.
- K danému F-součtu existuje jeden ekvivalent v nulové posloupnosti a jeden ekvivalent v určité základní posloupnosti.
- Dvě posloupnosti mají F-součty se stejnými indexy (a,b,c), pokud pro charakteristiky r(m) a r'(m) platí:
∑Δr(m)∙(  ) = 0; (m=0..k) ) = 0; (m=0..k)
|
kde Δr(m) = r'(m)−r(m) a
![]() ,
,
![]() ,
,
![]() jsou binomické koeficienty.
jsou binomické koeficienty.
Protože ( ) = 1−1−1 = −1,
můžeme z předchozího vztahu vyjádřit r(0):
) = 1−1−1 = −1,
můžeme z předchozího vztahu vyjádřit r(0):
∑Δr(0)= ∑Δr(m)∙( );
(m=1..k) );
(m=1..k)
|
Pro m=1 platí Δc(0)=Δc(1)∙(c−b−a). Pro (0,2,5) je c−b−a= 5−2−0=3.
F-součet s indexy (0,2,5) existuje tedy i v posloupnostech [1,1,12],[1,2,15],...,[2,1,21],[2,1,24], atd.
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[1,1,12] {12,13,15,18,22,27,33,..} ( 0, 2, 5) 12+15=27
[1,2,15] {15,17,20,24,29,35,42,..} ( 0, 2, 5) 15+20=35
[1,3,18] {18,21,25,30,36,43,51,..} ( 0, 2, 5) 18+25=43
[1,4,21] {21,25,30,36,43,51,60,..} ( 0, 2, 5) 21+30=51
────
[2,1,21] {21,22,25,30,37,46,57,..} ( 0, 2, 5) 21+25=46
[2,2,24] {24,26,30,36,44,54,66,..} ( 0, 2, 5) 24+30=54
[2,3,27] {27,30,35,42,51,62,75,..} ( 0, 2, 5) 27+35=62
─────
[3,1,30] {30,31,35,42,52,65,81,..} ( 0, 2, 5) 30+35=65
[3,2,33] {33,35,40,48,59,73,90,..} ( 0, 2, 5) 33+40=73
Podle uvedeného pravidla se pokusme vyhledat základní posloupnosti, ve kterých existují F-součty analogické vybraným pythagorejským F-součtům, tj. F-součtům (3,4,5), (6,8,10) a (5,12,13) z mocninné posloupnosti 2.řádu.
Budeme hledat taková r0, že platí transformační vztah pro převod posloupnosti s charakteristikami Rm=[2,1,0] na posloupnost Rz=[1,0,r0].
Rozdíl charakteristik činí ΔR=[1,0,r0]−[2,1,0]=[−1,−1,r0].
Platí:
Δr0=Δr2∙(
 )+Δr1∙(
)+Δr1∙(
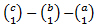 ).
).
Po dosazení dostáváme pro a=3,b=4,c=5: Δr0=+1,
pro a=6,b=8,c=10:Δr0=+2
a pro a=5,b=12,c=13 rovněž: Δr0=+2.
Proto základní posloupností pro F-součet s indexy (3,4,5) je:
[1,0,1] a pro F-součty s indexy (6,8,10) a (5,12,13): [1,0,2].
Charakter. Posloupnost F-součet
──────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,…} 9+16= 25
[1,0,1] {1,1,2,4,7,11,16,22,29,37,46,56,67,…} 4+7= 11
───────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,…} 36+64=100
[1,0,2] {2,2,3,5,8,12,17,23,30,38, 47, 57,… } 17+30= 47
───────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,…,81,100,121,144,…} 25+144=169
[1,0,2] {2,2,3,5,8,12,17,23,30,38,47,57,68,…} 12+ 68=80
───────────────────────────────────────────────────────────
Základní posloupnosti
Základní posloupnost řádu k má F-součet s indexy
(a,b,c) tehdy, když r0=
![]() −
−
![]() −
−
![]() .
.
To plyne přímo z transformace posloupnosti [0,0,0,...,0] do
[1,0,0,...,r0]
Např. F-součet s indexy (0,2,5) existuje v posloupnosti
s charakteristikou [1,0,9], neboť
r0=
![]() −
−
![]() −
−
![]() = 10−1−0 = 9.
= 10−1−0 = 9.
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[1,0,9] {9,9,10,12,15,19,24,...} ( 0, 2, 5) 9+10=19
Binomické posloupnosti
Posloupnost s charakteristikou [1,0,0] má členy f(a)=
![]() .
.
Charakter. Posloupnost F-indexy F-součet
───────────────────────────────────────────────────────────
[1,0,0] {0,0,1,3,6,10,15,21,...} ( 4, 6, 7) 6+15=21
Nabízí se otázka, pro která (a,b,c) v posloupnostech
řádu k existují F-součty
![]() +
+
![]() =
=
![]() ?
?
Pro k=2 až 5 dostáváme experimentálně tyto indexy:
- k=2: (4,6,7),(5,10,11),(6,15,16),..(6,7,9),(7,10,12),(10,22,24),(11,27,29),... (9,11,14),(10,14,17),(12,21,24),...(12,15,19), ...
- k=3: (10,16,17),(22,56,57),(32,57,60),(36,120,121), ...
- k=4: (132,190,200),..?
- k=5: ?
Např.
![]() +
+
![]() = 10 + 45 = 55 =
= 10 + 45 = 55 =
![]() .
.
Indexy v prvním řádku jsou tvaru (n,
![]() ,
,
![]() +1).
+1).
Posun posloupnosti
Změna charakteristiky r(m) o hodnotu v se projeví
posunem každého členu posloupnosti f(n) o hodnotu
![]() ∙v.
∙v.
Hodnotu m nazveme řádem posunu.
Např. pro k=3 - členy f(n) posloupností [6,6,1,v] jsou
vzhledem k posloupnosti [6,6,1,0] posunuty o hodnotu v∙
![]() = v:
= v:
Charakter. Posloupnost F-indexy F-součet
─────────────────────────────────────────────────────────
[6,6,1,0] {0,1, 8,27,64,125,216,..}
[6,6,1,1] {1,2, 9,28,65,126,217,..} ( 6,8,9) 217+513=730
[6,6,1,2] {2,3,10,29,66,127,218,..} ( 5,6,7) 127+218=345 Δ={1,1,1,1,1...}
Obdobně jsou také členy f(n) posloupnosti [6,6,v,0]
vzhledem k posloupnosti [6,6,0,0] posunuty o hodnotu
v∙
![]() = v∙n:
= v∙n:
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,6,0,0] {0,0, 6,24,60,120,…} ( 9,15,16) 720+3360=4080
[6,6,1,0] {0,1, 8,27,64,125,…}
[6,6,2,0] {0,2,10,30,68,130,…} (36,37,46) 46692+50690=97382 Δ={0,1,2,3,4...}
A členy f(n) posloupnosti [6,v,0,0] vzhledem k
posloupnosti [6,0,0,0] posunuty o hodnotu v∙
![]() :
:
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,0,0,0] {0,0,0,6,24,60,… } ( 0, 1, 2) 0+0=0
[6,1,0,0] {0,0,1,9,30,70,… } (11,19,20) 1045+5985=7030
[6,2,0,0] {0,0,2,12,36,80,…} (31,37,43) 27900+47952=75852 Δ={0,0,1,3,6,10...}
Posloupnosti charakteristik
Posloupností charakteristik p = {r} nazveme takovou posloupnost čísel r, které definují sledované charakteristiky - obvykle pro určité F-indexy.
Například budeme sledovat jaké charakteristiky [1,0,r] mají posloupnosti s F-indexy (0,b,c). Pro b=2 dostáváme posloupnost p2 = {0,2,5,9,14,20,27,...}:
Charakter. F-indexy F-součet Posloupnost
──────────────────────────────────────────────────────────
[1,0,0] (0,2,2) 0+1=1 {0,0,1,3,6,10,15,21,28,...}
[1,0,2] (0,2,3) 2+3=5 {2,2,3,5,8,12,17,23,30,...}
[1,0,5] (0,2,4) 5+6=11 {5,5,6,8,11,15,20,26,33,...}
[1,0,9] (0,2,5) 9+10=19 {9,9,10,12,15,19,24,30,37,...}
[1,0,14] (0,2,6) 14+15=29 {14,14,15,17,20,24,29,35,42,...}
[1,0,20] (0,2,7) 20+21=41 {20,20,21,23,26,30,35,41,48,...}
[1,0,27] (0,2,8) 27+28=55 {27,27,28,30,33,37,42,48,55,...}
Obecně pro F-indexy (0,b,c) jde o charakteristiky [1,0,r], kde r = [c2-c-(b2-b)]/2. Hodnotami F-součtů jsou přitom: [(c2-c)/2-(b2-b)/2] + [(c2-c)/2] = [(c2-c)-(b2-b)/2]. Např. pro F-indexy (0,3,4) vychází r = [42-4-(32-3)]/2 = 6/2 = 3 a součet 3 + 6 = 9:
Charakter. F-indexy F-součet Posloupnost
──────────────────────────────────────────────────────────
[1,0,3] (0,3,4) 3+6=9 {3,3,4,6,9,13,18,24,31,39,48,...}
[1,0,7] (0,3,5) 7+10=17 {7,7,8,10,13,17,22,28,35,43,52,...}
[1,0,12] (0,3,6) 12+15=27 {12,12,13,15,18,22,27,33,40,48,57,...}
Omezení charakteristik F-součtů
Zajímá nás, jaké vlastnosti musí mít posloupnost, aby v ní existoval F-součet. Některé případy jsou triviální; např. posloupnosti 0.řádu nemají nikdy F-součet, kromě případu r0=0. Tj. v posloupnosti 5,5,5,5,5,5,5.. nelze najít nikde číslo 5+5 = 10, ....
V dalších případech budeme sledovat jaký mají na existenci F-součtů vliv rozdílové posloupnosti.
Posloupnosti 1.řádu
Každou posloupnost 1.řádu můžeme zapsat ve tvaru:
f(n) = r1∙n+ r0; přitom r0 =
r1(c−b−a). Aby mohl F- součet existovat, musí být
číslo r0 dělitelné číslem r1 beze
zbytku:
Charakter. Posloupnost F-indexy F-součet
───────────────────────────────────────────────────────────
[1,0] {0,1,2,3,4,5,6,7,8,9,... } ( 1, 2, 3) 1+2=3
[1,1] {1,2,3,4,5,6,7,8,9,10,...} ( 0, 1, 2) 1+2=3
[1,2] {2,3,4,5,6,7,8,9,10,... } ( 0, 1, 3) 2+3=5
[1,3] {3,4,5,6,7,8,9,10,11,... } ( 0, 1, 4) 3+4=7
───────────────────────────────────────────────────────────
[2,0] {0,2,4,6,8,10,12,14,... } ( 1, 2, 3) 2+4=6
[2,1] {1,3,5,7,9,11,13,15,... }
[2,2] {2,4,6,8,10,12,14,16,... } ( 0, 1, 2) 2+4=6
[2,3] {3,5,7,9,11,13,15,17,... }
───────────────────────────────────────────────────────────
[3,0] {0,3,6,9,12,15,18,21,... } ( 1, 2, 3) 3+6=9
[3,1] {1,4,7,10,13,16,19,22,...}
[3,2] {2,5,8,11,14,17,20,23,...}
[3,3] {3,6,9,12,15,18,21,24,...} ( 0, 1, 2) 3+6=9
V posloupnostech 1.řádu mohou (potenciálně) existovat F-součty jen tehdy, když:
r0 ≡ 0 (mod r1)
Posloupnosti 2.řádu
V posloupnostech 2.řádu najdeme obdobný vztah:
r0≡0 mod (r1,r2)
kde (r1,r2) je největší společný dělitel čísel r1 a r2.
Např. pro r1 = 6 můžeme rozlišit následující případy:
(r1,r2) F-součty existují pro ──────────────────────────────────── (6,1)=1 všechny posloupnosti (6,2)=2 r0≡0 mod 2 (6,3)=3 r0≡0 mod 3 (6,4)=2 r0≡0 mod 2 (6,5)=1 všechny posloupnosti (6,6)=6 r0≡0 mod 6
Proto: V posloupnostech [6,8,r0] existuje F-součet tehdy, když r0≡0 mod (6,8), tj. když r0 je sudé.:
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,8,0] {0,8,22,42,68,100,138,...} ( 4,10,11) 68+350=418
[6,8,1] {1,9,23,43,69,101,139,...}
[6,8,2] {2,10,24,44,70,102,140,..} ( 3, 6, 7) 44+140=184
[6,8,3] {3,11,25,45,71,103,141,..}
[6,8,4] {4,12,26,46,72,104,142,..} ( 2, 3, 4) 26+46= 72
[6,8,5] {5,13,27,47,73,105,143,..}
[6,8,6] {6,14,28,48,74,106,144,..} ( 4,11,12) 74+424=498
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,6,0] {0,6,18,36,60,90,126,... } ( 3, 5, 6) 36+90=126
[6,6,1] {1,7,19,37,61,91,127,... }
[6,6,2] {2,8,20,38,62,92,128,... }
[6,6,3] {3,9,21,39,63,93,129,... }
[6,6,4] {4,10,22,40,64,94,130,...}
[6,6,5] {5,11,23,41,65,95,131,...}
[6,6,6] {6,12,24,42,66,96,132,...} ( 2, 3, 4) 24+42=66
Charakter. Posloupnost F-indexy F-součet
──────────────────────────────────────────────────────────
[6,7,0] {0,7,20,39,64,95,132,..} ( 7,28,29) 175+2464=2639
[6,7,1] {1,8,21,40,65,96,133,..} ( 6,21,22) 33+1408=1541
[6,7,2] {2,9,22,41,66,97,134,..} ( 5,15,16) 97+737= 834
[6,7,3] {3,10,23,42,67,98,135,.} ( 4,10,11) 67+343= 410
Obecnější kriterium
Obecný vztah získáme, když zapíšeme F-součet f(a)+f(b)=f(c) pomocí charakteristik posloupnosti. Např.
f(a)=r0∙
![]() +
r1∙
+
r1∙
![]() +
r2∙
+
r2∙
![]() + … = r0+
r1∙a+ r2∙a(a−1)/2+…
+ … = r0+
r1∙a+ r2∙a(a−1)/2+…
Po úpravách se objeví výrazy závislé na (c−b−a),(c²−b²−a²),... K zjednodušení zápisu zavedeme funkci d(m):
dm = d(m) = cm − bm − am
Např. pro posloupnost 3. řádu dostaneme vztah:
r0 + r1∙d1 + r2(d2−d1)/2 + r3(d3−3d2−2d1)/6 = 0
Pokud nějaké číslo dělí čísla r1,r2,r3,... musí dělit i r0, jinak není možné vztahu vyhovět. F-součty mohou existovat jen v posloupnostech s takovou charakteristikou, že platí:
r0≡ 0 mod (r1,r2,r3,...)
Nulové členy r1,r2,r3,... se z výpočtu největšího společného dělitele (r1,r2,r3,...) vynechávají.
V posloupnosti s charakteristikou [2,0,1] nemůže existovat F-součet, protože neplatí 1 ≡ 0 mod 2:
Charakter. Posloupnost Poznámka
───────────────────────────────────────────────────────
[2,0,1] {1,1,3,7,13,21,31,43,...} f(n) = n²−n+1
K posouzení platnosti Fermatovy věty toto kriterium ale nic nepřináší. U posloupností f(k) = ak je vždy r0 = 0.
Omezení indexů F-součtů
Transformace do nulové posloupnosti
Nulová posloupnost obsahuje F-součty s libovolnými indexy. Proto když existují F-součty v nějaké dané posloupnosti, existují k nim příslušné F-součty v nulové posloupnosti. A naopak v posloupnosti může existovat F-součet s indexy (a,b,c) jedině tehdy, pokud může být odvozen z nulové posloupnosti transformací pro dané (a,b,c).
Např. v posloupnosti [2,0,1] nemůže existovat žádný F-součet proto, že neexistuje žádné (a,b,c) k transformaci z [0,0,0] do [2,0,1]. Aby taková transformace existovala, muselo by být:
2∙(
 )=1,
tj. (c²−c) −(b²−b) −(a²−a)=1.
Číslo m²−m je ale pro každé mεZ sudé.
)=1,
tj. (c²−c) −(b²−b) −(a²−a)=1.
Číslo m²−m je ale pro každé mεZ sudé.
Takto získané vztahy se nijak neliší od vztahů
získaných rozpisem f(a)+f(b)=f(c) v předchozích odstavcích, o
mocninných posloupnostech se proto nedozvíme nic nového.
Např. z transformace [0,0,0] do [2,1,0] pro (a,b,c) zjistíme
jen, že má být c²−a²−b²=0, což je zjevné.
Transformace do základní posloupnosti
Pokusíme se najít základní posloupnosti, které mají F-součty se stejnými indexy jako dané mocninné posloupnosti. Přitom budeme předpokládat, že pokud k dané posloupnosti s F-součtem s indexy (a,b,c) neexistuje základní posloupnost se stejnými indexy F-součtu, tak F-součet (a,b,c) není v dané posloupnosti možný.
V posloupnostech 2.řádu z transformace [2,1,0] do [1,0,r0] plyne:
2∙r0 = (c²−b²−a²) − (c−b−a) = d2−d1
Protože je zároveň d2=0 (tj. a²+b²=c²) tak:
2∙r0 = −d(1) = −d(1) = −(c−b−a) = a+b−c
Pro indexy F-součtů mocninné posloupnosti 2.řádu musí proto platit:
−d1 ≡0 mod 2 tj. j+i−c≡0 mod 2
Tento vztah v pythagorejských trojúhelnících platí, např. 3+4−5≡0 mod 2, 5+12−13≡0 mod 2, ...
Z transformací mezi posloupnostmi vyšších řádů najdeme obdobné vztahy:
Řád Vztah ─────────────────────────────────────────── 2 −d1 ≡0 mod 2 3 −3∙d2+2∙d1 ≡ 0 mod 6 4 −6∙d3+11∙d2−6∙d1 ≡ 0 mod 24 5 −10∙d4+35∙d3−50∙d2+24∙d1 ≡ 0 mod 120
Čísla u jednotlivých d(m) jsou Stirlingova čísla prvního druhu s(k,m), viz Rekurentní posloupnosti.
Obecnější kriterium
K mocninné posloupnosti k-tého řádu s indexem F-součtu (a,b,c) existuje základní posloupnost s charakteristikou [1,0,...,0,r0], když platí k!∙r0 = ∑ s(k,m)∙d(m), kde d(m)=rm−bm−am.
Pro indexy F-součtu (a,b,c) v mocninných posloupnostech k-tého řádu proto musí platit:
∑ s(k,m)∙d(m) ≡ 0 (mod k!)
V opačném případě by neexistovala k dané posloupnosti odpovídající základní posloupnost se stejnými indexy F-součtů.
Např. indexy (1,2,4) nemohou být řešením a³+b³=c³ protože:
d1= c−b−a= 4−2−1 = 1, d2= c²−b²−a²= 16−4−1= 11, −3∙d2+2∙d1 = −33+2 = −31
a −31 není dělitelné 6 (tj. není kongruentní b 0 podle modulu k!=3!=6).
Uvedené vztahy můžeme přepsat také do tvaru:
δc− δb− δa ≡0 mod k! kde δa = a(a−1)(a−2)..(a−k+1).