Konjunkce, nerovnosti

Úvod

Ze tří možností pro vyčíslení časových údajů využijeme především "matematický" a "historický" způsob. 

historicky      astronomicky     matematicky
-------------------------------------------
1.4.2005 AD       2005(.25)         2005.25
1.4.   1 AD          1(.25)            1.25
1.4.   1 BC          0(.25)            0.25
1.4.   2 BC         -1(.25)           -0.75
1.4.2005 BC      -2004(.25)        -2003.75

Synodická perioda

Periody pohybu

Základní orbitální periody těles se udávají vzhledem k hvězdám. Jsou to tzv. siderické (hvězdné) periody.

K dalším výpočtům budeme používat střední periody podle VSOP87. (Bretagnon, Variations Seculaires des Orbites Planetaires):

Vnějších planet

Vnitřních planet 

J  11.8620 let   ( 4332.59 dní)
S  29.457159 let (10759.23 dní)
U  84.020473 let (30688.48 dní)
N 164.770132 let (60182.29 dní)

M   0.2408467 let ( 87.96926 dní)
V   0.6151973 let (224.70080 dní)
E   1.0000174 let (365.25636 dní)
R   1.8808480 let (686.97973 dní)

Konjunkce

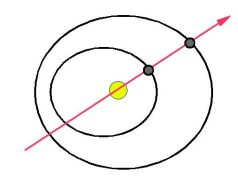c_synod Konjunkce je těsné přiblížení až zarovnání (splynutí) dvou či více těles. Pro jednoduchost budeme uvažovat jen zarovnání těles do jedné roviny kolmé na rovinu, v níž se planety přibližně pohybují (tzv. konjunkci v délce). Přesná zarovnání do jedné přímky nástávají zřídka a bývají studována obvykle v souvislosti s jinými jevy (zatmění Slunce a Měsíce, přechody Merkuru a Venuše přes sluneční kotouč,...)

Pozorujeme-li těleza ze Slunce mluvíme o heliocentrické konjunkci (konjunkci se Sluncem).
Např. leží-li v jedné přímce tělesa v pořadí Slunce-Venuše-Země-Mars, říkáme že Venuše-Země, Země-Mars, Venuše-Mars i Venuše-Země-Mars jsou v konjunkci (při pohledu ze Slunce).

V praktické astronomii se konjunkcí rozumí zpravidla geocentrická konjunkce. Jsou-li Slunce-Venuše-Země-Mars v jedné přímce, říká se, že Venuše je v konjunkci a Mars v opozici (se Sluncem při pozorování ze Země).

Synodická perioda dvou těles

Průměrná perioda s jakou se opakují (helio)centrické konjunkce dvou těles se nazývá synodická perioda.

Synodická (vztažná) perioda dvou orbitálních period P,Q je perioda:

 (P,Q) = 1/(1/P-1/Q)= P∙Q/(Q-P) 

Synodickou periodu značíme kulatými závorkami ().

Pro libovolné periody A,B a konstantu k platí:

(A,B) = -(B,A) (k∙A,k∙B) = k∙(A,B) ((A,M),(B,M)) = (A,B).


V praktické astronomii bývá mlčky předpokládáno, že jednou z period je oběžná perioda Země. Např. synodická perioda Jupitera se udává cca 399 dní. Jde o periodu Jupitera vzhledem k Zemi: (E,J) = (365.256,4332.59) = 398.9 dní.
Se synodickou periodou se postupně rozvírá (a pak zase přivírá) úhel P-S-Q; S je bod (centrum) okolo kterého tělesa P,Q obíhají.

Párové synodické periody planet

Vnějších planet

Vnitřních planet 

(J,N)= 12.7822 let ( 4668.69 dní)
(J,U)= 13.8120 let ( 5044.81 dní)
(J,S)= 19.8589 let ( 7253.45 dní)
(S,N)= 35.8699 let (13101.47 dní)
(S,U)= 45.3602 let (16567.82 dní)
(U,N)=171.4443 let (62620.01 dní)

(M,R)= 0.276217 let (100.8882 dní)
(M,E)= 0.317255 let (115.8775 dní)
(M,V)= 0.395801 let (144.5662 dní)
(V,R)= 0.914227 let (333.9215 dní)
(V,E)= 1.598690 let (583.9214 dní)
(E,R)= 2.135349 let (779.9361 dní)

Synodický den

Synodický den je rotační perioda Tr měřená vzhledem k oběžné periodě T, tj. synodická perioda (Tr,T).

V případě oběžnic Slunce se mluví o “slunečním dnu”, např. má-li Země rotační periodu Tr =1 hvězdný (siderický) den, je její sluneční den roven

(1.0, 365.256) = 1.0027 hvězdných dní. Sluneční den dělíme na 24 hodin.

Přepólování

Mějme několik menších period Pi: (P0, P1,..., Pn), a větší periodu Q. Pokud periody Pi mají společný násobek P, který je přibližně rovný Q, bude se nám zdát, že celá soustava má periodu P. To však samozdřejmě není pravda. Odchylky period (P-Q) se budou postupně hromadit; v průběhu synodické periody (P,Q).

Takové hromadění odchylek se může jevit jako proměna cyklu P, jako změna jeho polarity.

Např. periody 3,4 a 13 let tvoří společný násobek cca 12-13 let. Tuto je možné dobře aproximovat periodou P=12 let. Ale po delším čase zaregistrujeme rázy s periodou periodou cca (12,13)=156 let.

Ve sluneční soustavě - periody (U,N)= 171.44 let a 9∙(J,S)=178.730 se liší o více než 7 let. Přesto bývají společně pokrývány tzv.180-ti letou periodou.

Odchylky period (U,N) a 9∙(J,S)  oscilují cca s periodou (9∙(J,S),(U,N))=(178.7, 171.4)=4200 let.

Periodu cca 4400 let  (resp. její harmonické 2200 let a 1100 let), našla I.Charvátová v pohybu těžiště Sluneční soustavy. Podle I.Charvátové činí základní interval cca 55 konjunkcí (J,S), tj. 1100 let. Pozorované odchylky charakteristik pohybu jsou střídavě kladné a záporné (intervaly v letech): (-2200,-1100) +; (-1100,0) -; (0,+1100) +; (+1100,+2200) -.

Cyklus velkých konjunkcí

Zkreslení

Uvedená definice konjunkce není fyzikálně správná, jde jen o geometrickou konstrukci. Odhlížíme od konečné rychlosti světla stejně jako od deformací časoprostorových vztahů apod.
Např. k porovnání konjunkcí V-E (perioda 1.6 let) s konjunkcemi J-N (perioda 12.8 let), je nutné uvažovat prostorovou odlehlost přibližně 29 AU. (Tuto vzdálenost cca 4.3∙1012 m proběhne světlo za cca 14300 sekund, tj. za cca 4 hodiny...)

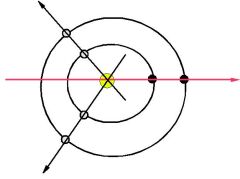
c_ineq

Interakce Venuše-Země

Čtyřletá perioda

Za čtyři roky je dokončena právě polovina pětilístku který vzniká vzájemným pohybem Venuše a Země. Perioda byla nalezena v řadě biologických i ekonomických jevů. Znaly ji staří Řekové (perioda olympiád), i Mayové (cyklus 4 pojmenování dnů). Podle Wooda existuje cyklus měsíčních přílivů v trvání 4.001 let.

Osmiletá perioda
Perioda 16-ti letá

Interní cyklus

„Interním“ cyklem nazýváme cyklus vnitřních planet s periodou I=6.4 let.

Perioda I

Rezonance 3:4:7 synodických period Venuše, Země a Marsu:

Perioda 6.4 let

Náznak pravidelnosti

Konjunkce Venuše-Země-Mars se opakují přibližně každých 6.4 let. Za 4 konjunkce V-E proběhnou 3 konjunkce E-R. Tento pohyb se děje desítky let s pravidelností hodinového stroje. 

 V-E        E-R
 ---------  --------
 1886.140   1886.181
 1887.728
            1888.281
 1889.335     
            1890.406
 1890.929

 V-E        E-R
 ---------  --------
 1892.528   1892.593
 1894.132
            1894.806
 1895.720
            1896.949
 1897.330

  V-E       E-R
 ---------  --------
 1898.923   1899.055
 1900.520
            1901.147
 1902.127     
            1903.241
 1903.715

 V-E        E-R
 ---------  --------
 1905.322   1905.352
 ....         ....

Kdyby byly konjunkce slyšitelné, zvuk by připomínal bubeníka, který hraje na čtyři taktové doby tři trioly (taktovými dobami jsou přitom konjunkce Venuše se Zemí).

6.394758 let: 4∙(V,E) = 4∙1.5986896 let,  6.399591 let: 7∙(V,R) = 7∙0.9142273 let, 6.406046 let: 3∙(E,R) = 3∙2.1353487 let

(E,R)/(V,E)= 779.9361 dní/583.9214 dní= 2.1353487 let/1.5986896 let= 1.335687.

  (E,R)/(V,E) ~  4/3 

Chybějící smyčka? 

V-E         E-R 
----------- ----------- 
2039.6081   2040.0078 
2041.2152 
            2042.1051 
2042.8032 
            2044.1968 
2044.4104 
----------- ----------- 
2046.0066   2046.2968 
2047.6000 
            2048.4269 
2049.2099 
            2050.6200 
2050.7979 
----------- ----------- 
2052.4023   2052.8267 
...

Pravidelnost konjunkcí V-E-R se po cca 150-ti letech docela vytratí (viz výpis vpravo):

Celý cyklus se opakuje s periodou cca 300 let.

Poměr (E,R)/(V,E) není 4/3 (192/144), ale spíše 191/143. Po cca 300 letech jedna konjunkce V-E i jedna E-R "vypadne": 191∙ 1.5986896 let = 305.350 let, 143∙ 2.1353487 let = 305.355 let

Tedy: (E,R)/(V,E) = (4∙48-1)/(3∙48-1); 48∙((V,E),(E,R)) = 48∙ 6.361133 let = 305.334 let


Mayové udávají periodu: 140∙(E,R)= 140∙780 dní = 109200 dní (299 let=23∙13 let), nebo 187∙(V,E).
V tomto případě: (E,R)/(V,E) = (4∙47-1)/(3∙47-1).

Podobně je také: (4∙(E,R))/((V,E),(E,R)) = (4∙12-1)/(3∙12-1) a R/Ey=(2∙54-1)/54=107/54, viz Ekliptický rok.

Přímkové konfigurace

Okamžiky, kdy spojnice Země-Venuše-Mars tvoří přímku, se opakují také (obdobně jako konjunkce) přibližně s periodou 6.4 let. Zde se ale ukazuje ještě jiná struktura.

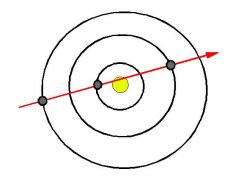
c_mloop

Mars zůstane čtyřikrát (3 periody R) na témže místě. Později (po 6.4 letech od počátku) tentýž vzor začne znovu (fázový posun F je cca 250-300 dní).
Nechť: 3∙R + F = 6.4 y. Pak F = 6.4 - 3∙1.880848 = 0.757 let = 276.7 dní.

c_rve1 
 Datum       (Interval) Čas
-----------------------------------
 1885 Mar 29 (1.88364) 1885.24820
 1887 Feb  9 (1.86721) 1887.11545
 1889 Jan  3 (1.90007) 1889.01556
 1889 Oct  1 (0.74196) 1889.75754
 1891 Aug 23 (1.89185) 1891.64943
 1893 Jul  8 (1.87543) 1893.52490
 1895 Jun  5 (1.90828) 1895.43322
 1896 Feb 10 (0.68446) 1896.11770
 1897 Dec 29 (1.88364) 1898.00138
 1899 Nov 17 (1.88364) 1899.88506
 1901 Oct  9 (1.89185) 1901.77696
 1902 Jul 31 (0.80767) 1902.58464
 1904 Jun 18 (1.88364) 1904.46832
 ...

Každých cca 300 let jedna perioda R "vypadne", tedy celý jeden cyklus 6.4 let za cca 1020 let (300 let∙6.4/1.88)?

Perioda 12.8 let

Mayská perioda 13 tun

Perioda 13*18*20 dní = 4680 dní (12.81 let).

13 Mayských tunů = Dvojnásobná perioda konjunkcí V-E-R:

8*(V,E) = 12.789516 let = 2* 6.394758 let6*(E,R) = 12.812088 let = 2* 6.406044 letMayský cyklus 18 tzolkin: 18*z= 4680 dní= 12.81 let([J,N],U)= 12.74 let(J,N)= 4668.7 dní= 12.78 let(U/2,S/3)= 12.81 let,...

Mars v přísluní

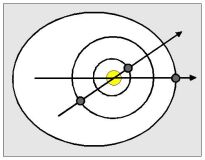
c_loop32

Protože frac(6.4/1.88)= 2/5, pozorovatel Marsu s periodou 6.4 let zjistí, že Mars vytváří pětiúhelník podobně jako konjunkce V-E,  frac(1.6/1.0) = 3/5. Opozice V-E, Mars v perihelu: 

 Rozdíl   Datum     Lv   Le    Lr    Lv-Le 
-------------------------------------------- 
 ( 31.98) 1715.86:  47.6 228.2 326.0 -180.6 
 ( 31.98) 1747.84:  38.7 219.9 326.6 -181.1 
 ( 31.98) 1779.81:  29.9 211.5 327.2 -181.6 
 ( 31.98) 1811.79:  21.2 203.2 327.8 -182.0 
 ( 31.97) 1843.76:  12.1 194.2 328.2 -182.1 
 ( 31.98) 1875.74:   3.5 185.8 328.8 -182.3 
 ( 31.98) 1907.72: 354.9 177.4 329.4  177.5 
 ( 31.98) 1939.69: 346.3 168.9 330.0  177.4 
 ( 31.98) 1971.67: 337.8 160.5 330.6  177.3
Perioda 32-letá

Konjunkce V-E opakují svou pozici vzhledem k Zemi každých 8 let a konjunkce V-E-R nastávají s periodou 6.4 let. Tedy konjunkce V-E-R nastává přibližně na témže místě vzhledem k Zemi po 32 letech: 32 let = 3∙10.67 let, 32 let = 4∙8.00 let, 32 let = 5∙6.40 let.

Náhled z Marsu

Pozorováno z Marsu: Venuše se stáčí s periodou (V,R/3)= 32.819643 let po směru, zatímco Země se pohybuje zpětně s periodou (E,R/2)= 15.780949 let.

Výsledný pohyb dává periodu: [32.819643, 15.780949] = 10.656765 let. ((V,R),E) = 10.6567 let = 31.97/3 let. Pět period (E,R): 5∙(E,R) = 10.676744 let.
Rovnost by nastala tehdy, pokud by byla splněna nestabilní rezonance: 5/V  - 6/E - 4/R = 0 (1139 let).

Pozn.:Modulace (10.656765, 302.4347) = 11.046 let.

Jiné periody

Perioda 256 let

Mayská perioda. Třináct Mayských katunů je 256.3 let.

Trojité konjunkce J-S (pozorovány ze Země) se vrací po 257-258 letech; např. r. 333, 411, 452, 710, 967, 1008, 1306, 1425, ...

Začlenění Marsu

Marsova excentrická dráha by měla být v souladu s pohybem Jupitera i pohybem ostatních vnitřních planet.

Rezonance rázů

Z celočíselných poměrů párů Merkur-Země (E/M=4/1) a Venuše-Mars (R/V=3/1) dostáváme rázy:
kde R2/R1 ~ 5/1.  Odtud (nestabilní) rezonance s rázy (M, V/5, E/4, R/15):

 1/M-5/V-4/E+15/R = 0 

Výraz Lx = Lm - 5*Lv - 4*Le + 15*Lr,  kde Lm, Lv, Le a Lr jsou longitudy planet M,V,E a R,
opakuje hodnoty přibližně s periodou Marsu.
Hodnoty Lx
Například hodnoty  Lx + 45  ~ 0° v čase průchodu Marsu perihelem jsou v následující tabulce.    0
Lx+45 1909,62 1922,79 1935,95 1949,12 1962,28 1975,45 1988,62 2001,78 2014,95
0 0 29,2 353,3 0,3 16,6 333,2 347,2 26,8 341,0 352,3
+1,88 0 2,5 353,7 23,6 359,9 336,7 4,0 359,2 341,0 17,6
+3,76 0 330,4 9,7 26,4 342,5 0,9 8,1 330,3 355,1 23,1
+5,64 0 339,0 23,4 351,4 355,7 23,3 341,5 337,9 7,6 350,2
+7,52 0 3,4 14,4 331,3 15,4 20,7 334,0 0,9 0,0 330,9
+9,40 0 25,3 340,1 341,3 27,2 345,4 354,9 20,2 327,1 341,7
+11,28 0 17,9 338,5 2,1 7,1 335,4 18,4 10,4 327,3 2,3
Vztah ale neplatí přesně, dlouhodobě dochází k pozvolnému stáčení longitudy Lx proti směru pohybu planet.
Sedmiúhelník
Z výrazu  5/V-15/R = 2/7R plyne, že se úhel    5*Lv-15*Lr v čase průchodu Marsu perihelem
postupně posouvá o 360° * 2/7, to jest tvoří sedmiúhelník.
5*Lv-15*Lr 1909,62 1922,79 1935,95 1949,12 1962,28 1975,45 1988,62 2001,78 2014,95
0 0.00 345,9 341,3 347,9 351,3 347,9 357,7 353,0 358,0 1,3
+1,88 102,86 89,2 85,1 92,1 93,2 92,1 100,5 95,2 102,9 103,5
+3,76 205,71 193,0 187,8 196,7 194,9 196,0 203,0 198,3 207,5 205,2
+5,64 308,57 295,3 289,7 300,5 296,5 300,7 305,7 301,6 311,1 307,0
+7,52 51,42 37,3 34,5 43,9 39,1 45,5 47,5 45,2 54,2 49,4
+9,40 154,28 138,7 138,8 147,1 140,3 149,8 149,0 149,3 157,2 151,8
+11,28 257,14 240,8 242,1 249,5 244,6 253,9 250,9 253,8 259,3 254,6

Nerovnosti

c_ineq

Perioda nerovnosti

Dvě tělesa P a Q opakují své pozice (např. v konjunkci na tomtéž místě) tehdy, když q period P je rovno p periodám Q, tedy když:  q∙P = p∙Q, resp. P/Q=p/q, kde p,q jsou celá čísla.

Nechť

 q/Q -p/P = 1/I 

Perioda I se nazývá perioda nerovnosti (nerovnost, angl.inequality):

 I = (Q/q,P/p) = P∙Q/(q∙P-p∙Q) 

Obvykle je I řádově větší než P a Q (I>>P, I>>Q).

S periodou I se stáčí místo, kde planety P a Q opakují své pozice.

Velký trojúhelník

Konjunkce planet J a S se objevují v průměru každých 19.859 let. Za tuto dobu urazí Jupiter přibližně: (J,S)/J ∙360° = 1.67416∙360 = 360+242.698°.  A Saturn přibližně: (J,S)/S ∙360° = 0.67416∙360 = 242.698°. Protože 240°=(2/3)*360° vytváří místa konjunkcí rovnostranný, tzv. velký trojúhelník. Tento trojúhelník se stočí za 19.859 let o ((J,S)/S - 2/3)∙360° = 242.698-240 = 2.698°.

Po 120°/2.698 ∙ 19.859, tj. cca po 900 letech (velká nerovnost) se v počátečním místě objeví druhý vrchol, po cca 1800 letech třetí. Celý trojúhelník se dotočí do své původní polohy po cca 2700 letech.

Kdyby nedocházelo ke stáčení, mířila by každé 3∙(J,S) konjunkční přímka tímtéž směrem. Tedy i po 42∙(J,S), 45∙(J,S) či 48∙(J,S). Za tuto dobu (cca 900 let) se trojúhelník stočí přibližně o 120° vpřed. Tedy konjunční přímka ukazuje tímtéž směrem každých cca 43, 46, či 49 konjunkcí.

43∙(J,S) = 853.9 let, 46∙(J,S) = 913.5 let, 49∙(J,S) = 973.1 let

Lambert, Johann Heinrich
Lambert, Johann Heinrich, 1728-1777 německý fyzik matematik a astronom. Zabýval se perspektivou, sférickou trigonometrií, kartografií, fotometrií, odrazem a rozptylem světla, algebrou.

Změna rychlosti planet

J.H.Lambert si povšiml, že střední rychlost Saturna se oproti rychlosti z Galileových měření zvýšila. Tuto odchylku vysvětlil za nedlouho poté Laplace efektem malých jmenovatelů.

Velká nerovnost

Hodnota nerovnosti Jupiter-Saturn (tzv. velká nerovnost, Laplaceova perioda, ...) není známa s velkou přesností. Předpokládá se, že jde o periodu "okolo 900 let" (840-960 let?).

Z Bretagnonových dat (J=11.8620 let, S=29.457158) vychází: I = (J/2,S/5) = -883.3 let.

S/1

S/2

S/3

S/4

S/5

S/6

S/7

S/8

J/1

19.859

60.947

57.013

19.422

11.705

8.376

6.522

5.340

J/2

7.426

9.929

14.978

30.474

883.27

28.507

14.487

9.711

J/3

4.567

5.405

6.620

8.538

12.024

20.316

65.464

53.556

J/4

3.298

3.713

4.249

4.965

5.971

7.489

10.042

15.237

J/5

2.580

2.828

3.128

3.500

3.972

4.591

5.438

6.670

J/6

2.119

2.284

2.475

2.703

2.976

3.310

3.729

4.269

Podle hodnot Ptolemaiových (J=11.862923, S=29.465040) je: I = (J/2,S/5) = -909.0 let.

Pohled ze Země

Země se kývá s periodou P, cca 25500-26000 let. Pohyb planet se proto jeví zkreslený. Odpovídající "zkreslené" periody se nazývají tropické periody. Nechť P=25750 let. Pak J' = (11.8620, 25750) = 11.85652 let a S' = (29.457158, 25750) = 29.42350 let.

Za 19.859 let  se velký trojúhelník stočí o ((J',S')/S' - 2/3)∙360° = 242.976°-240° = 2.976°.

Po 120°/2.976 ∙ 19.859, tj. po cca 800 letech (velká nerovnost z pohledu Země) se v počátečním místě objeví druhý vrchol, po cca 1600 letech třetí. Celý trojúhelník se dotočí do své původní polohy po cca 2400 letech.

S/1

S/2

S/3

S/4

S/5

S/6

S/7

S/8

J/1

19.8589

61.0913

56.7618

19.3784

11.6836

8.3628

6.5120

5.3319

J/2

7.4241

9.9294

14.9870

30.5457

800.940

28.3809

14.4464

9.6892

J/3

4.5654

5.4039

6.6196

8.5412

12.0347

20.3638

66.1358

53.0054

J/4

3.2962

3.7120

4.2479

4.9647

5.9725

7.4935

10.0541

15.2728

J/5

2.5792

2.8270

3.1274

3.4994

3.9718

4.5916

5.4406

6.6748

J/6

2.1184

2.2827

2.4747

2.7019

2.9751

3.3098

3.7293

4.2706

Při pohledu ze Země se zdají tropické periody být ty jediné správné. Při výpočtu odvozených period si ale musíme počínat dostatečně obezřetně. Nepatrný rozdíl tropických a siderických period působí v našem příkladě velký rozdíl výsledků (2400 let vs. 2700 let, viz výše).

(Některé hodnoty v tabulce, např. 3.4994, 14.9870, vychází blízko celočíselným zlomkům pozemského roku. Hodnota (J/3,S/4)=8.5412 let je rovna ekliptickému roku Y).

Laplaceův cyklus

Cyklus přibližně 900-letý (840-960 let?) vytvářený tzv. velkou nerovností planet Jupiter a Saturn.
G. Beutler v knize Methods of Celestial Mechanics uvádí periodu 890 let ,
prof. A.E.Roy píše v knize Orbital motion o 900-leté oscilaci. 
Poslední extrémy Laplaceova cyklu byly přibližně v letech 1560 (minimum) a 2000 (maximum).

Synchronizace perihelů

Mayský kalendářní kruh (52 let) a počítání tunů (1-18)  spoluvytváří periodu 9 Aztéckých století tj. 9*102 = 936 let.

S toutéž periodou se synchronizují perihelia Jupitera a Saturna. Hodnota (Ja/2,Sa/5) počítaná z anomalistických period Ja,Sa  činí cca 938-939 let.

Laplaceova perioda

Perioda byla pozorována v následujících jevech:

Střední denní pohyb 

Hodnoty nP=360/P jsou obecně nazývány Střední úhlové rychlosti ( Mean Angular Velocities, MAV), viz Angular velocity.
Jestliže je perioda P dána ve dnech, mluvíme o Středním denním pohybu ( Mean Day Motion, MDM).  

Jestliže planeta obíhá v daném okamžiku se střední rychlostí, je její pohyb někdy nazýván "pravý pohyb" ("true motion", střední pohyb).  Jestliže je planeta ve stavu pravého (středního) pohybu, je její aktuální perioda rovna střední periodě. Skutečná rychlost pohybu se odchyluje od rychlosti pravého (středního)  pohybu.

Přesnost

Přesnost antických astronomických nástrojů nebyla lepší než cca 10’ (0.167 dg) - v porovnání s tím přesnost hodnot v době Edmunda Halleye dosahovala 10”.
Nicméně přesnost některých výsledků v antice byla velmi vysoká, např . Hipparchos určil MDM Země s přesností 0.0435” (0.000012 dg).  Hodnoty MDM dané v Almagestu (Claudius Ptolemaios) vedou -po korekci precese - k následujícím MDM pro Jupiter a Saturn: nJ=299,104581“ nS=120,422528“.  Tyto hodnoty odpovídají  periodám J=3600/299,104581 * 360/365,25 = 11.862923 let a S =3600/120,422528 * 360/365,25 = 29.465040 let.
Bretagnonova teorie (VSOP) dává tyto hodnoty MDM: <nJ>=299.1283“ and <nS>=120.4547“, tj. periody : J=11.861983 let, S=29.457159 let. 
Pro rok 2000  uvádí NASA tyto aktuální hodnoty MDM  : nJ=299.1124“ a nS=120.4943“.  

Perioda (I) nerovnosti Jupiter –Saturn se získá z poměru S:J v blízkosti rezonance 5:2:  I(J,S) = 1/(5/S-2/J) . Protože jmenovatel je malý, závisí výsledná hodnota silně na přesnosti středních oběžných period Jupitera a Saturna. Z Bretagnonových dat I(11.861983, 29.457158) = 883.3 let, z dat Ptolemaia I(11. 862923, 29.465040) = 909.0 let.

Bretagnonovy hodnoty

Střední pohyb Jupitera jev Bretagnonově VSOP82 teorii definován řádkem: LM = { 0.5995465, 52.969096500,-15e-7, 0.0}.
Zde hodnota 52.9690965 určuje změnu střední délky za století v radiánech: 
Odtud J  =  360 * 100 / (52.9690965 * 180/PI) = 36000/3034.905674=11.8619832 let. 
Hodnota value -15e-7 je term druhého řádu (dlohodobá změna).  Poruchy jsou počítány zvlášť. 

V teorii VSOP87 je pro totéž (včetně poruch) 915 termů, které musí být vyčísleny a sečteny pro jednu polohu Jupitera. Zde jsou první 3 termy, kde první řádka s délkou 0.599546 odpovídá hodnotě LM výše. V druhé řádce je term pro velkou nerovnost, třetí řádka patří rezonanci S/J = 2/1:
J   S   A     B    C   
1/   0  0    0.59954649739 0.00000000000   0.00000000000  
2/   2 -5    0.00573506125 1.44396306420   7.11354700080  
3/   1 -2    0.00062308554 3.41857056095     103.09277421860 

Pak následují další řádky. 17-tý řádek reprezentuje střední pohyb Jupitera, kde hodnota 529.69096509460 (v radiánech za tisíciletí)  je:  
17/  1  0    0.00001824700 5.72883078185     529.69096509460 

Odtud dostáváme střední periodu Jupitera: 
J= 360 * 1000 / (529.69096509460 * 180/PI) = 36000/3034.905674=11.8619831585 let. 
Pak následuje ještě 900 dalších termů. Hodnoty A, B a C v řádku se dosazují do vzorce  v= A* Cos(B+ C*t) a sčítají, tedy hodnoty s malým A příliš výsledek neovlivňují.   

Tedy, periody mou být počítány z hodnot C v řádcích podle vztahu:
T = 2000PI/ C = 6283.1853/ C.  
Pro velkou nerovnost tak dostaneme: 6283.1853/7.113547 = 883.27 let. 
Pro rezonanci S/J = 2/1 je 6283.1853/103.09277 = 60.9469 let 
(povšimněme se, že je to Čínská 60-ti letá perioda modulovaná celým cyklem trojúhelníku konjuncí J-S: 
1/60.9469 = 1/59.579 – 1/2649.1).  

Objev harmonické vlny

Náhodné odchylky ve středních pohybech Jupitera a Saturnu našel   ( v roce 1637) anglický astronom Jeremiah Horrocks (1619 – 1641). Edmunt Halley (1656-1742) si povšiml, že MAV Jupitera (Saturnu) se zvýšila (snížila)  v porovnání s antickými  hodnotami. Teorie planetárního pohybu založená na Newtonových zákonech pak došla k vzorci postupné změny : nJ = 299.1283611” – 0.000 000 089 81” T, nS = 120.4546453” + 0.000 002 836” T, 
kde T je čas měřený v Julianských stoletích (36525 dní) od 0 Ledna 1850 (antické hodnoty pro T=-20).

Edmund Halley dále upřesnil hodnotu pro Saturn na nS=120.4054”, potvrdil, že se  MDM Saturna (v porovnání s antikou) snížila a vyslovil názor, že změna je způsobena vzájemnými gravitačními poruchami Jupitera a Saturnu..
Johann Lambert (1728-1777) zjistil, že MDM Saturna se zvýšila v porovnání Halleyovou hodnotou o 0,02” (Saturn zrychlil) - a odtud začalo být jasné, že pozorovaný jev není postupná změna, ale harmonická vlna.

Podle pozorování 18.století bylo nJ=299,128361“, nS=120,454645“ a tedy 2nJ-5nS=-4,016503” (=-0,0000194725 rad). 
Pierre-Simon Laplace odvodil dlouhodobou harmonickou funkci (s hodnotou 2nJ-5nS ve jmenovateli)
a vypočítal, že se teoretické výsledky (které tuto funkci nezahrnuji) mohou odlišovat od skutečných poloh planet o 20’ (0.33 dg) pro Jupiter a o 50’ (téměř 1 dg) pro Saturn.

Sinusoida

Předpokládejme, že Jupiter i Saturn byly ve stavu pravého (středního) pohybu v roce <t> = 1780 a že se vzájemně ovlivňují s Laplaceovou periodou I  = 4*220 = 880 let.  Bretagnonovy hodnoty středního pohybu jsou <nJ>=299.1283“, <nS>=120.4547“. 
Tyto hodnoty MDM pak můžeme přiřadit k rokům: -3500,-2620,-1740,-860,20,900,1780,2660,… 
a také k jejich středům:  -3060,-2180,-1300,-420,460,1340,2220,…
Rok 2000  je 220 let  po roce 1780 a pro tento rok máme NASA hodnoty (nJ=299.1124“, nS=120.4943“). 
Stejné hodnoty můžeme očekávat i v letech:  -3280,-2400,-1520,-640,240,1120,2000,2880,…

Definujme funkce:    
        Q = sin[ (t - <t>) * 2PI / I ],       
        nJ =   <nJ> - <aJ> *  Q,     
        nS =   <nS> + <aS> * Q 
a z uvedených hodnot (pro 2000 a 1780) vypočítejme amplitudy: 
        <aJ> = 299.1283“- 299.1124“ =0.0159“  and  <aS> = 120.4943“- 120.4547“ =0.0396“.

Nyní dosadíme všechny známé hodnoty: 
         Q = sin[ (t - 1780) * 2PI / 880 ],  
        nJ =   299.1283“ - 0.0159“ *  Q,   
        nS =   120.4547“ + 0.0396“ *  Q 

Pro roky 1340, 1560, 1780 a 2000 dostaneme tyto MDM hodnoty a aktuální (oskulační) periody.

Rok Q nJ nS Roky J S
1340  0 299.1283“ 120.4547“ -3060,-2180,-1300,-420,460,1340,2220 11.8620 y 29.4572 y
1560 -1 299.1442“ 120.4151“ -2840,-1960,-1080,-200,680,1560,2440 11.8614 y 29.4669 y
1780 0 299.1283“ 120.4547“ -2620,-1740,-860,20,900,1780,2660 11.8620 y 29.4572 y
2000 1 299.1124“ 120.4943“ -2400,-1520,-640,240,1120,2000,2880 11.8626 y 29.4475 y
Amplitudy

Jestliže jsou amplitudy <aJ>=0.0159“ and <aS>=0.0396“ změnami MDM, pak za rok dosáhnou přibližně:  <AJ>=0.0159“ * 365.25 =5.81“ a <AS>=0.0396“ * 365.25 = 14.46“ 

 Maximální odchylka od střední hodnoty se objevuje cca po 220-ti letech:
<AJ,max>= 5.81“*220 =1278“ and  <AS,max>= 14.46“*220=3181“
Tyto hodnoty odpovídají 1278“/60=21.3‘ pro Jupiter a 3181“/60=53.0‘ pro Saturn.
M.Somerville udává 19.78‘ a 48.04‘, Paul Schlyter 19.92‘ a 48.72‘.  

Energie

Někteří vědci uvažují o spojení Laplaceova cyklu s pozorovaným tisíciletým cyklem sluneční aktivity.
Pokud Jupiter získá - pro své vlastní urychlení - nějakou dodatečnou energii od Slunce , pak by ztráta sluneční energie mohla být pozorována. Roky v nichž  Q nabývá hodnoty -1: -9000,-8120,-7240,-6360,-5480,-4600,-3720,-2840,-1960,-1080,-200,680,1560,2440,… 
Rok 1560 odpovídá tzv. Suessovu minimu.


V letech 691 a 1561 nastala opozice Uranu proti ostatním vnějším planetám (rozdíl 870 let):

syst06910821o syst15611022o

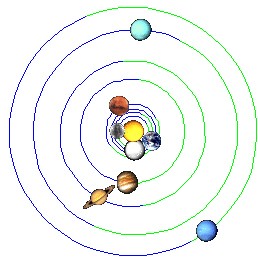
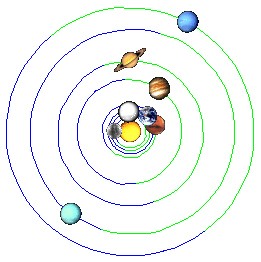
Sluneční rotace

Synodická rotační perioda Slunce pozorovaná ze Země byla stanovena cca 27.275 dní.
V některých letech dříve (~Maunderovo minimum) byla nižší.

1611-13 26,163 dní
1625-26 24,913 dní
1642-44 24,300 dní